물의 pKa + α

유의사항

이 글에서는 물의 $\text{p}K_{\text{a}}$가 $15.7$이 아닌 $14.0$임을 주장하고 있습니다. 유기화학 과제나 시험 등에서는 선생님/교수님을 충분히 설득하지 않는 이상 수업에서 배운 값을 사용하시기 바랍니다.

이 글은 세 출처를 기반으로 작성되었습니다.

물의 $\text{p}K_{\text{a}}$에 관하여:

• What is the pKa of water? on LibreTexts
• pKa Values in the Undergraduate Curriculum: What Is the Real pKa of Water? by Silverstein and Heller, published in the Journal of Chemical Education

일반적인 $\text{p}K_{\text{a}}$에 관하여:

• pKa Values in the Undergraduate Curriculum: Introducing pKa Values Measured in DMSO to Illustrate Solvent Effects by Silverstein and Heller

14.0인가 15.7인가

거의 모든 일반화학 서적에 따르면 물의 $\text{p}K_{\text{a}}$는 $14.0$입니다¹. 하지만 대부분의 유기화학 서적과 자료에서는 물의 $\text{p}K_{\text{a}}$가 $15.7$이라고 합니다.

아래는 David Klein 저 Organic Chemistry에서의 한 예시입니다.

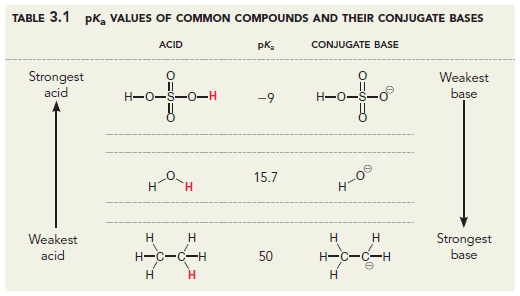
또 유기화학자 사이에서 널리 쓰이는 Ripin과 Evans의 $\text{p}K_{\text{a}}$표도 그렇고요.

이 값은 다음과 같은 방법으로 유도할 수 있습니다². 먼저 각 화학종의 활동도(activity, $a$)³로 산 해리 상수(acid dissociation constant, $K_\text{a}$)를 쓰면

\[K_\text{a} = \frac{a_{\text{H}^{+}} a_{\text{OH}^{-}}}{a_{\text{H}_2\text{O}}}\]

묽은 용액의 경우 활동도를 몰 농도로 근사할 수 있습니다⁴. 따라서 $a_{\text{H}^{+}} = \left [ \text{H}^{+} \right ]$이고 $a_{\text{OH}^{-}} = \left [ \text{OH}^{-} \right ]$입니다. 또한 순수한 물의 경우 $\left [ \text{H}^{+} \right ] = 1.0 \times 10^{-7} \, \text{M}$이며 $\left [ \text{OH}^{-} \right ] = 1.0 \times 10^{-7} \, \text{M}$입니다.

최종적으로 남은 변수는 $a_{\text{H}_2\text{O}}$입니다. 물을 용매로 생각하여 이 값을 $1$로 설정하는 것 대신 물을 용질이라 생각하여 물의 몰 농도를 활동도에 대입할 것입니다.

물의 몰 농도를 구해봅시다. 물의 분자량은 $18.015 \, \text{g/mol}$이며 밀도는 $25 ^{\circ} \text{C}$에서 $997 \, \text{g/L}$입니다. 따라서 물의 몰 농도는 $ \left [ \text{H}_{2}\text{O} \right ]$는 $55.3 \, \text{M}$입니다. 이 값을 물의 활동도에 대입하면 $\text{p} K _{\text{a}} = 15.7 $이라는 값을 얻게 됩니다.

위 유도식은 총 세 가지 이유로 틀렸습니다.

1. 물의 활동도는 단순히 $1$입니다: 기준 상태의 순수한 물질은 활동도가 $1$로 정의되기 때문이지요.
2. 용매인 물을 용질로 취급하는 것, 그리고 이에 따라 물의 ‘농도’를 계산하는 것은 용납하기 어렵습니다.
3. 설령 용납하더라도 $ \left [ \text{H}_{2}\text{O} \right ] = 55.3 \text{M}$는 묽은 용액으로 가정하기에 너무 큽니다. 따라서 활동도를 몰 농도로 근사하는 것 또한 불가능합니다.

참으로 어리석은 실수이지 않을 수 없습니다. 하지만 왜 이 잘못된 $\text{p}K_{\text{a}}$ 너무나도 널리 받아들여졌을까요? 이는 위에서 소개해드린 “What is the pKa of water?”글에서 더 자세히 알 수 있습니다. 간단하게 설명하자면 이 실수는 브뢴스테드(Brønsted) 같은 유망한 화학자들도 여러분처럼 햇갈리면서 시작된, 그런 역사와 전통이 있는 실수입니다. 그 이후 어떤 물리유기화학자들이 물의 $\text{p}K_{\text{a}}$를 간접적으로 계산하려다 정확히 똑같은 실수를 범하였으며, 이런 오류가 제대로 검증되지 않고 수많은 출판물과 서적과 $\text{p}K_{\text{a}}$표에 그대로 실리게 되었습니다. 이로 인해 유기화학을 배우는 수천만의 학생들이 헷갈린 것은 덤이고요.

물의 $\text{p}K_{\text{a}}$를 유도하는 옳은 방법은 $\left [ \text{H}^{+} \right ] = 1.0 \times 10^{-7} \text{M}$와 $\left [ \text{OH}^{-} \right ] = 1.0 \times 10^{-7} \text{M}$ 값의 대입부터 이어집니다.

\[K_\text{a} = \frac{1.0 \times 10^{-14}}{a_{\text{H}_{2}\text{O}}} = 1.0 \times 10^{-14}\]

이때 물의 활동도는 아시다시피 $1$입니다. 이 ‘$1$’은 계산에 아무 의미가 없지만, 화학적인 의미는 지대합니다. 이는 물이 ‘기준 상태’인 순수한 액체로 존재함을 내포하며, 따라서 $\text{p}K_{\text{a}} = 14.0$이라는 값은 필연적으로 물이 용질이 아니라 용매임을 암시합니다. 계속해서 용매를 강조해왔지만 이는 앞으로도 끊임없이 강조할 부분입니다.

물은 용매이면서 산이다

비록 물의 $\text{p}K_{\text{a}}$가 $14.0$임을 위에서 확정지었지만 이 값을 활용할 때는 특히 주의해야 합니다. 아래 예시를 한 번 봅시다.

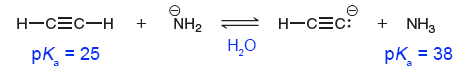
아세틸렌의 $\text{p}K_{\text{a}}$가 암모니아의 $\text{p}K_{\text{a}}$보다 더 작으며, 따라서 아세틸렌은 암모니아보다 더 강한 산입니다. 참 쉽죠?

더 구체적으로는 위 $\text{p}K_{\text{a}}$값들이 물이 용매임을 가정하기에 물에서 아세틸렌이 암모니아보다 더 강한 산입니다.

다른 예시를 봅시다.

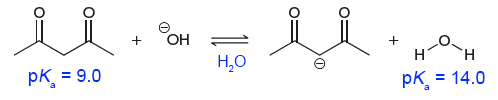
이 경우에는 acetylacetone(좌측의 1,3-diketone)은 용매이며 산으로 작용하는 물보다 더 강한 산입니다. 만일 acetylacetone과 산/용질로만 고려되는 물의 세기를 비교하고 싶다면 물이 아닌 다른 용매에서 비교해야 합니다.

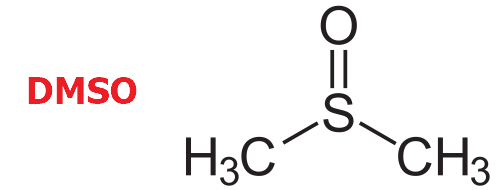
Dimethyl sulfoxide(DMSO) 용매계에서 acetylacetone과 물은 새로운 $\text{p}K_{\text{a}}$를 갖게 됩니다. 일반적으로 이 새 $\text{p}K_{\text{a}}$도 단순히 $\text{p}K_{\text{a}}$라고 지칭하나 헷갈리지 않도록 특별히 $\text{p}K_{\text{a}}^{\ast}$라고 지칭하겠습니다.

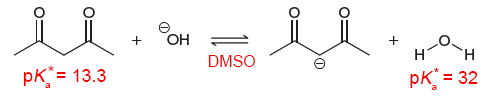
Acetylacetone과 물의 $ \text{p} K_{\text{a}}^{\ast} $를 통하여 acetylacetone이 산/용질로 작용하는 물보다 더 강한 산임을 알 수 있습니다.

한 단점

다른 용매계에서 산의 세기를 비교하는 방법의 가장 큰 단점은 일부 산에 대하여 산의 세기의 순서가 뒤바뀔 수 있다는 점입니다.

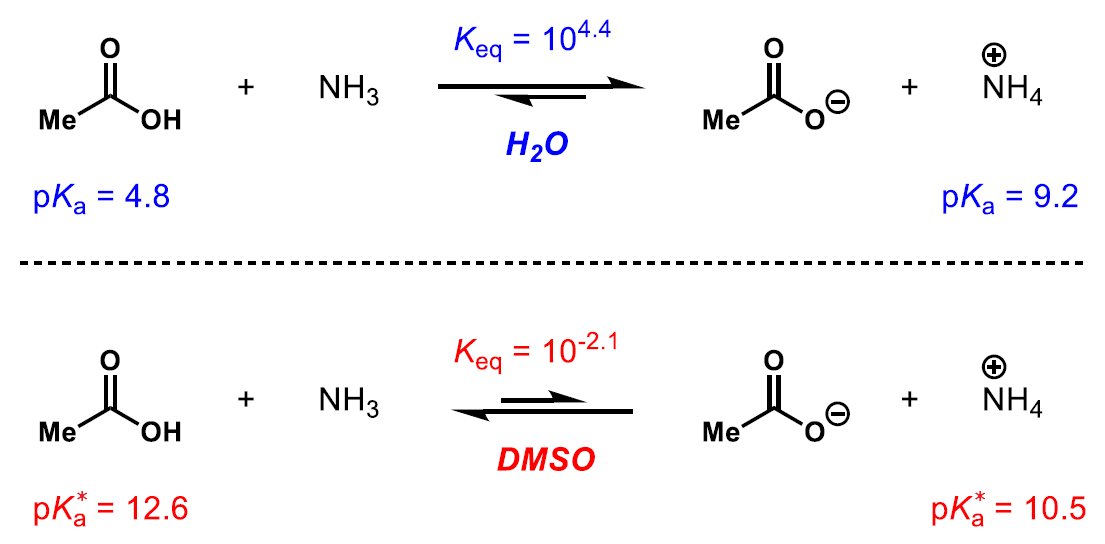
예를 들어 물에서 아세트산은 암모늄 이온보다 더 강한 산입니다(위 화학평형). 하지만 DMSO에서는 암모늄 이온이 아세트산보다 더 강한 산이며(아래 화학평형), 보시는 것과 같이 산의 세기의 순서가 반대입니다.

pKa ≠ 산의 세기?

유기화학에서는 산의 세기가 그 산의 고유한 성질이라고 배우게 되며 $\text{p}K_{\text{a}}$이 성질의 척도로 사용됩니다. 하지만 위에서 보여준 예시와 같이 산의 세기는 산의 고유한 성질이 아니며 용질 등 여러 요소에 영향을 받습니다. 물을 용매로 한 $\text{p}K_{\text{a}}$를 다른 용매(예를 들어 DMSO)를 사용하는 상황에서는 적용하는 것은 실수로 볼 수 있습니다.

하지만 이 실수가 큰 문제는 되지 않습니다. 아래는 $\text{p}K_{\text{a}}$와 $\text{p}K_{\text{a}}^{\ast}$의 그래프입니다. 대체로 $\text{p}K_{\text{a}}$가 증가할 때 $\text{p}K_{\text{a}}^{\ast}$ 또한 증가하는 것이 보입니다. 즉, 한 용매계에서 강산은 다른 용매계에서 강산이며, 다른 용매계에서 약산은 다른 용매계에서 약산임은 분명합니다.

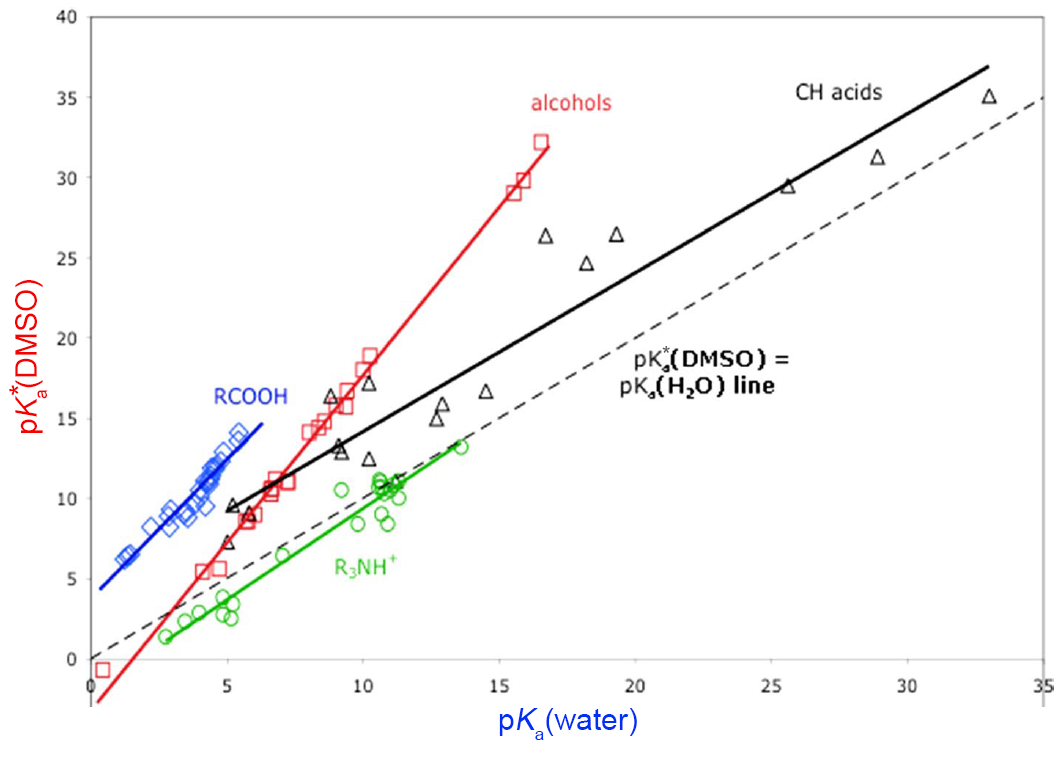
간단히 정리하자면:

메탄올과 아세트산과 같은 극성 양성자성 용매(polar protic solvent)의 경우 $\text{p}K_{\text{a}}$는 산의 세기를 예측하는 데 매우 좋은 척도입니다. 이는 모든 극성 양성자성 용매에 화학종이 비슷한 양상으로 용해되기 때문이지요.

아세톤이나 THF와 같은 극성 비양성자성 용매(polar aprotic solvent)의 경우 $\text{p}K_{\text{a}}$는 산의 세기를 예측하는 데 나쁘지 않은 척도입니다. 하지만 이런 목적으로는 $\text{p}K_{\text{a}}^{\ast}$가 월등히 좋으며 가능하다면 극성 비양성자성 용매를 다룰 때 $\text{p}K_{\text{a}}$ 대신 $\text{p}K_{\text{a}}^{\ast}$를 사용하는 것이 좋습니다.

결론

1. (물을 용매로 하는) 물의 $\text{p}K_{\text{a}}$는 $15.7$가 아니라 $14.0$이다.
2. ‘동시에 용매와 산으로 작용하는 물’과 ‘산으로만 작용하는 물’의 산의 세기는 별개이다.
3. 산의 세기는 고유한 성질이 아니며, 용매에 의해 큰 영향을 받는다.

추가 문헌

다양한 용매계에서의 산-염기 평형을 다룬 책이 있으며, 궁금하시다면 한 번 보시는 것도 추천해 드립니다.

• Acids and Bases: Solvent Effects on Acid-Base Strength by Brian G. Cox

각주

1. $25 ^{\circ} \text{C}$, 출처에 따라 $ 1 \, \text{atm}$ 또는 $1 \, \text{bar}$. ↩

2. 이 글에서 소개된 방법 말고도 다른 다양한 방법으로 $\text{p}K_{\text{a}} = 15.7$를 유도할 수 있습니다. 매우 엄밀한 $\text{p}K_{\text{a}} = 14.0$의 유도 과정을 포함한 더 완전한 설명은 “What is the pKa of water?”에서 찾으실 수 있습니다. ↩

3. 활동도는 화학종의 ‘실질적 농도’라고 볼 수 있습니다. 더 자세하게 알고 싶으시다면 이 글을 찾아보시길 바랍니다. ↩

4. 활동도를 몰 농도로 근사하는 과정을 더 엄밀하게 설명하자면 다음 공식을 사용해야 합니다: $a = \gamma \frac{c}{c^{\circ}}$. $\gamma$는 용매, 용질, 농도 등의 영향을 받는 활동도 계수이며 농도가 $0 \, \text{M}$에 접근할 때 (무한하게 희석할 때) $1$에 수렴하게 됩니다. $c$는 몰 농도이고 $c^{\circ}$ 는 기준 상태이며 주로 $1 \, \text{M}$로 정의합니다. 활동도 $a$는 차원이 없는 값이며 따라서 일반화학에서 배웠듯이 모든 평형 상수 또한 차원이 없습니다. ↩