Atomic Term Symbols: 파트 1 - 선행지식

개요

이 글은 원자 term symbol를 소개하고 설명하는 글이며 McQuarrie의 Physical Chemistry: A Molecular Approach 8장을 보충하기 위해 작성되었습니다. 부가적으로 사용된 출처는 Levine의 Quantum Chemistry이며 이해를 위해서는 Physical Chemistry: A Molecular Approach 6장과 7장에 대한 전반적인 이해가 요구됩니다.

이 글에 사용된 표기는 대부분 Physical Chemistry: A Molecular Approach와 일치합니다.

파트 1은 다전자 원자의 양자역학적 특성을 다루며, 파트 2와 3은 term symbol을 본격적으로 다룹니다.

원자의 Hamiltonian

다전자 원자를 논하기 위해서 우선 다전자 원자의 Hamiltonian을 알아야 합니다. 전자 $n$개와 $Z$의 핵전하를 가진 원자의 Hamiltonian은 atomic unit으로 다음과 같습니다.

\[\hat{H} = \sum_{i\,=\,1}^{n}\left ( -\frac{1}{2}\nabla_i^2 \right ) + \sum_{i\,=\,1}^{n}\left ( -\frac{Z}{r_i} \right ) + \sum_{i}\sum_{j\,>\,i} \left ( \frac{1}{r_{ij}} \right )\]

위의 $\hat{H}$의 퍼텐셜 에너지 항에는 오직 쿨롱 상호작용만 포함되어 있습니다. Spin-orbit coupling(스핀-궤도 결합)과 같은 상호작용은 영향이 작아 지금으로선 무시하도록 합니다.¹

$\hat{H}$의 eigenfunction을 $\psi \left(r_1, \theta_1, \phi_1, \sigma_1;\,r_2, \theta_2, \phi_2, \sigma_2;\, \cdots ;\,r_n, \theta_n, \phi_n, \sigma_n \right)$²이라고 하면 이 $\psi$는 다전자 원자의 에너지 상태입니다. 이런 $\psi$는 수치적인 방법으로 또는 Hartree-Fock self-consistent-field (SCF) 방법과 같은 근사법으로 구할 수 있습니다.

하지만 다전자 원자의 특성을 논하기 위해서는 $\psi$의 함수꼴을 정확히 알 필요는 없습니다. 가장 중요한 점은 $\psi$가 $\hat{H}$의 eigenfunction이라는 점이며 앞으로 $\hat{H}$와 $\psi$의 특성을 알아보고자 합니다.

Complete Set of Commuting Observables

수소꼴 원자의 $\psi$는 당연하게도 원자 오비탈입니다. 아시다시피 수소꼴 원자의 $\hat{H}$는 궤도 각운동량 연산자 $\bold{\hat{l}}$와 commute하지 않고 $\bold{\hat{l}}$의 제곱인 $\hat{l}^2$과 commute합니다.³ 이로 인하여 $\psi$는 $\hat{H}$와 $\hat{l}^2$의 eigenfunction이 동시에 되게끔 선택할 수 있으며, 만약 $\hat{H}$의 eigenfunction인 어떤 $\psi$가 $\hat{l}^2$의 eigenfunction이 아니라도 $\psi$와 다른 파동함수의 적당한 선형 결합을 통하여 $\hat{H}$와 $\hat{l}^2$의 eigenfunction인 다른 파동함수를 만들 수 있습니다.

이의 물리학적 의의는 $\psi$로 서술되는 에너지 상태가 확실한 $\left| \bold{l} \right|^2$ 값과 $E$(에너지) 값을 가진다는 것을 의미합니다. 참고로 이런 관측될 수 있는 값을 observable(가관측량)이라고 합니다.

$\bold{\hat{l}}$의 z-성분인 $\hat{l}_z$는 $\hat{l}^2$와 유사하게 $\hat{H}$와 commute합니다. 또한 $\hat{l}_z$와 $\hat{l}^2$는 서로 commute합니다. 따라서 $\psi$는 $\hat{H}$, $\hat{l}^2$, 그리고 $\hat{l}_z$의 eigenfunction이 동시에 될 수 있으며 물리적으로는 이 에너지 상태는 확실한 $E$, $\left| \bold{l} \right|^2$, 그리고 $l_z$ 값을 가진다는 것을 의미합니다.

전자 스핀 연산도 이와 비슷합니다. $\hat{s}^2$와 $\hat{s}_z$³는 $\hat{H}$와 commute하며 이는 $\hat{H}$가 전자 스핀에 의존성이 없기 때문입니다. $\hat{s}^2$와 $\hat{s}_z$는 서로 commute합니다(더 정확히 말하자면 이 두 연산자는 서로 commute하도록 정의됩니다). 두 궤도 각운동량 연산자($\hat{l}^2$ 또는 $\hat{l}_z$) 중 하나와 두 스핀 연산자($\hat{s}^2$ 또는 $\hat{s}_z$) 중 하나를 고르면 그 두 연산자는 무조건 서로 commute하며, 이는 전자는 공간 좌표에만 의존하고 후자는 스핀 좌표에만 의존하기 때문입니다.

따라서 연산자 $\hat{H}$, $\hat{l}^2$, $\hat{l}_z$, $\hat{s}^2$, $\hat{s}_z$는 아래 도식과 같이 모두 서로 commute합니다.

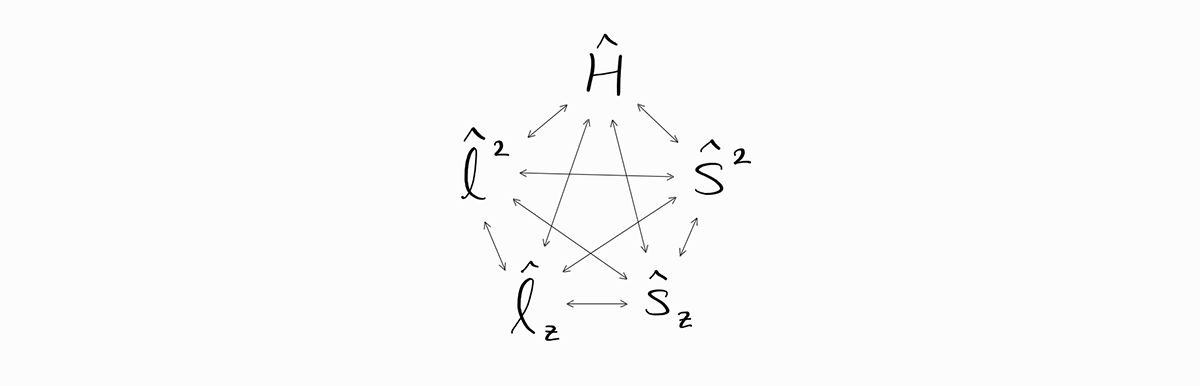
수학적으로 이는 특정 파동함수 $\psi$는 $\hat{H}$, $\hat{l}^2$, $\hat{l}_z$, $\hat{s}^2$, $\hat{s}_z$의 eigenfunction이며 아래 관계식을 만족함을 의미합니다.

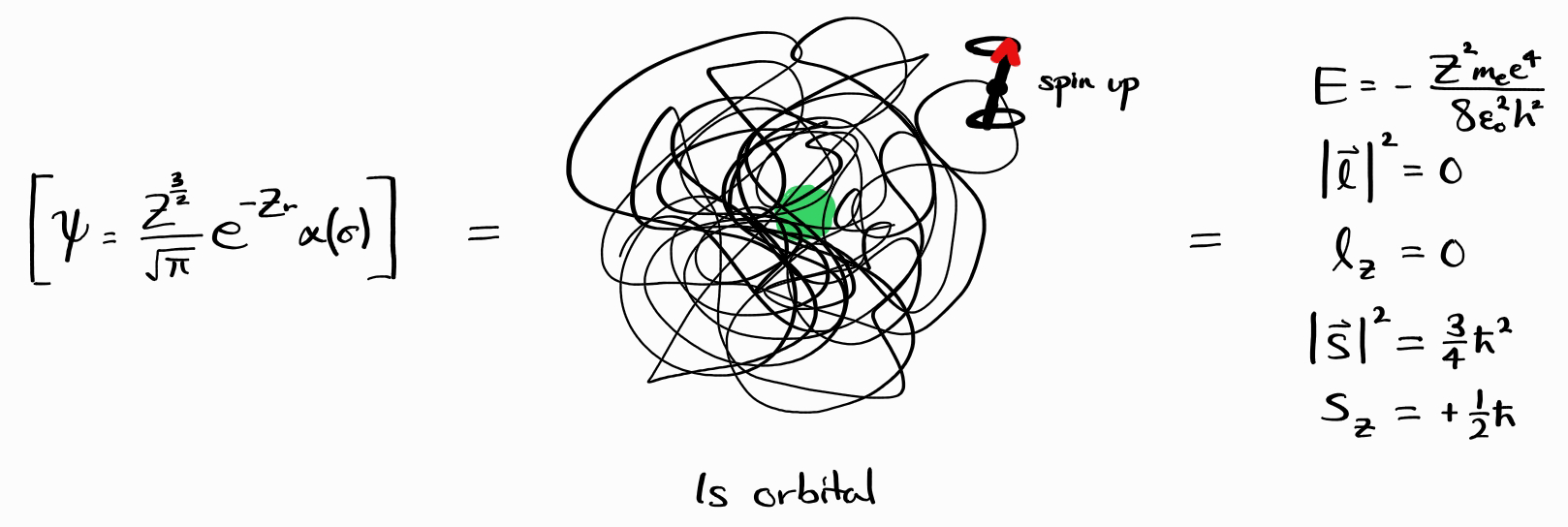
\[\hat{H} \psi = E \psi\] \[\hat{l}^2 \psi = \left| \bold{l} \right|^2 \psi\] \[\hat{l}_z \psi = l_z \psi\] \[\hat{s}^2 \psi = \left| \bold{s} \right|^2 \psi\] \[\hat{s}_z \psi = s_z \psi\]

이의 물리학적 의미를 살펴보면 이런 에너지 상태는 확정적인 $E$, $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$, $s_z$ observable 값을 가집니다. 예를 들어 파동함수 $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \alpha(\sigma)$ ($1s$ 오비탈에 전자 1개가 스핀 업 상태로 있다는 것을 말합니다)의 observable은 SI 단위계로 $E = -Z^2 m_e e^4/8\epsilon_0^2h^2$, $\left| \bold{l} \right|^2 = 0$, $l_z = 0$, $\left| \bold{s} \right|^2 = 3\hbar^2/4$, $s_z = +\hbar/2$입니다.

다전자 원자의 모든 에너지 상태는 특정 $E$, $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$, $s_z$을 가진, degenerate한 에너지 상태의 선형 결합으로 만들어질 수 있습니다. 이의 예로는 파동함수 $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \times \frac{1}{\sqrt{2}}\left(\alpha(\sigma) + \beta(\sigma)\right)$를 들 수 있습니다.

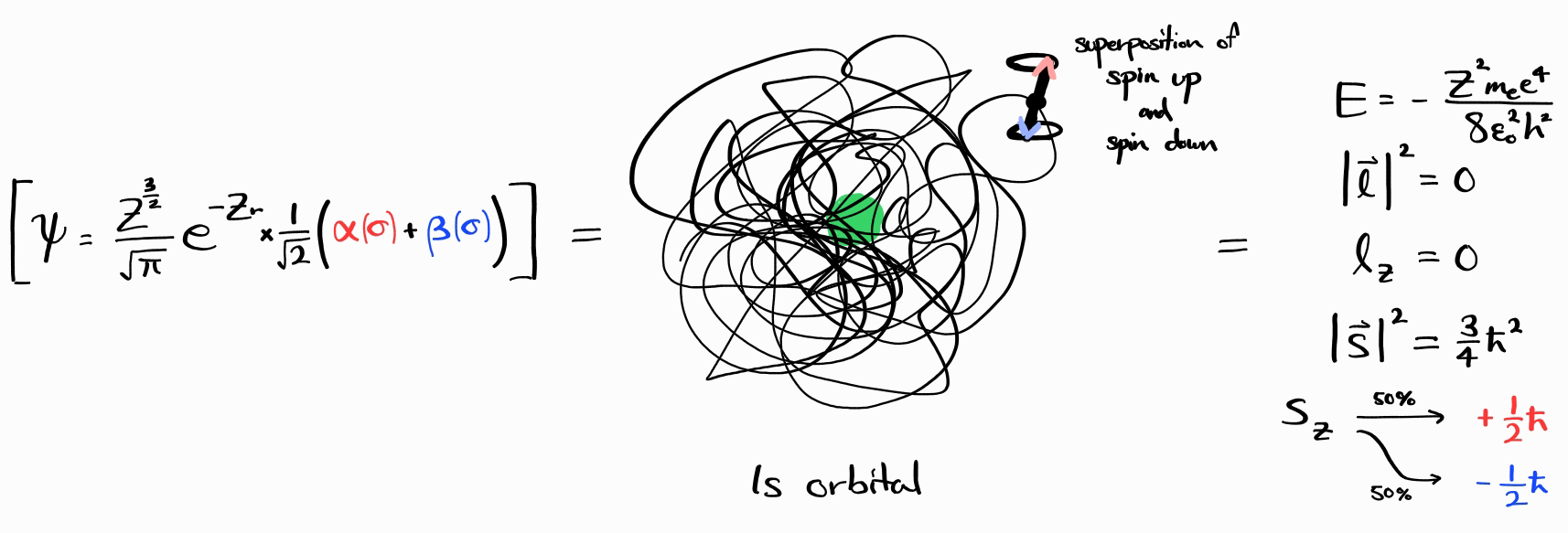
이 파동함수는 $E$는 위의 예시와 같으며 특정한 값을 가지기에 에너지 상태입니다. 이 파동함수의 $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$ 또한 위의 예시와 같습니다.

하지만 전자의 스핀($s_z$)은 특정 값을 가지지 않으며, 이는 spin up ($\alpha(\sigma)$, $s_z = +\frac{\hbar}{2}$)과 스핀 다운 ($\beta(\sigma)$, $s_z = -\frac{\hbar}{2}$)의 superposition(중첩)이기 때문입니다. $s_z$를 관측하였을 때 50% 확률로 spin up이며 나머지 50% 확률로 스핀 다운입니다.

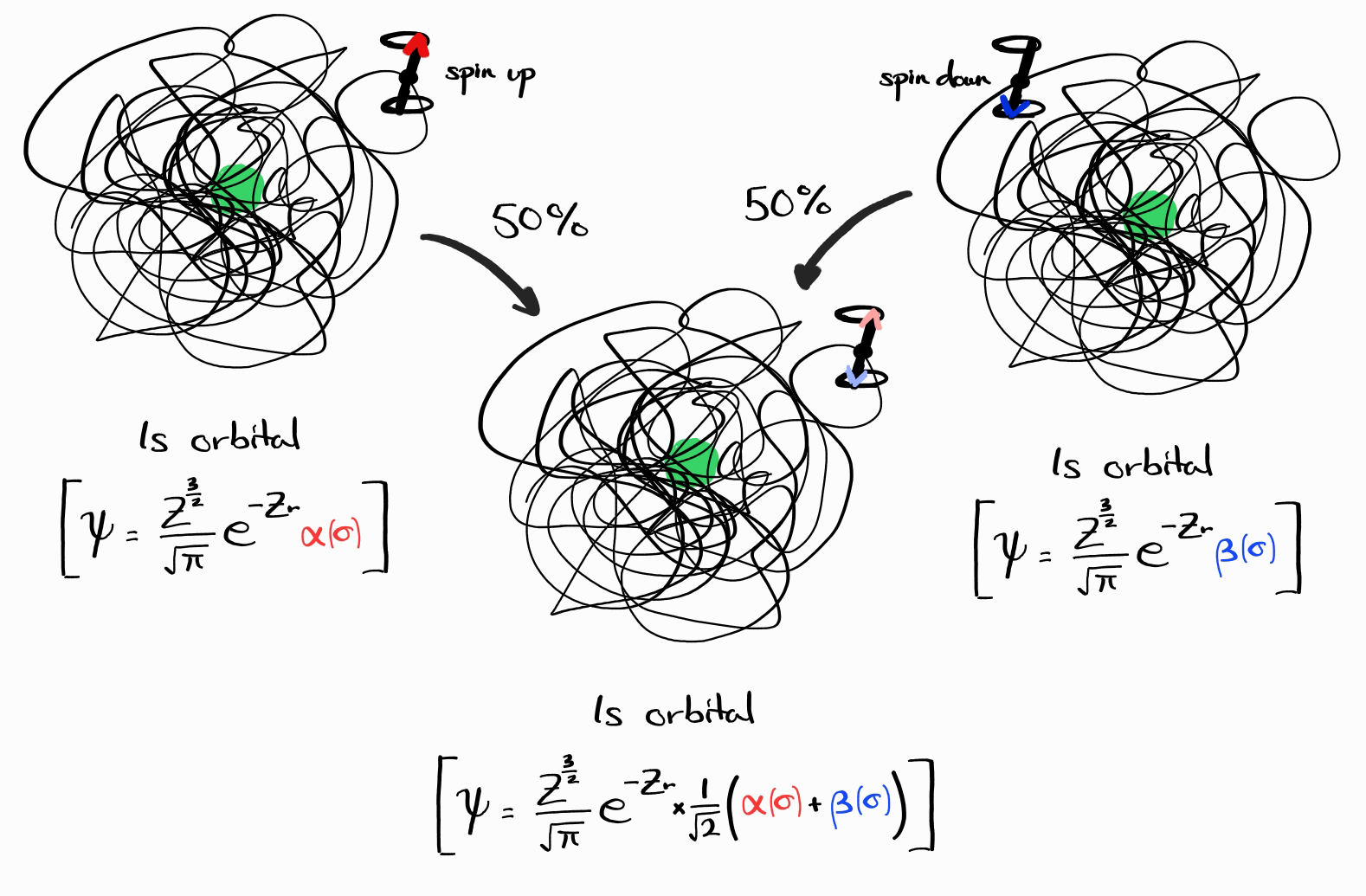
이와 비슷한 예시는 사실 무한하게 많습니다. 하지만, 이 가능한 모든 파동함수는 특정 $E$, $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$, $s_z$ 값을 지니는 파동함수의 선형결합으로 나타낼 수 있습니다. $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \times \frac{1}{\sqrt{2}}\left(\alpha(\sigma) + \beta(\sigma)\right)$의 경우 이는 $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \alpha(\sigma)$ (항상 spin up)과 $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \beta(\sigma)$ (항상 스핀 다운)의 선형결합입니다. 수학적으로 이 두 함수는 $\hat{H}$의 eigenbasis 중 일부라고 할 수 있습니다.

양자역학의 다양한 현상을 설명할 때 $E$, $\left| \bold{l} \right|^2$, $\cdots$, 등 observable이 특정되는 파동함수로 설명하는 것이 그러하지 않은 파동함수로 설명하는 것보다 훨씬 쉽고 이해하기에도 편합니다. 예를 들어 간단한 질문인 “이 에너지 준위의 degeneracy(같은 에너지를 가진 에너지 상태의 개수)는 얼마인가요?”를 묻는다면 엄밀한 정답은 다음과 같을 것입니다.

무수히 많은 에너지 상태의 에너지가 같지만, 그러한 에너지 상태는 모두 서로 다른 두 개의 독립적인 파동함수 (예를 들어 $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \alpha(\sigma)$와 $\psi = \frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \beta(\sigma)$)로 분해될 수 있습니다.

이는

이 에너지 준위의 degeneracy는 2입니다.

라고 말하는 것보다 거추장스럽다는 것을 보실 수 있습니다.

따라서, 앞으로는 편의와 가독성을 위해 모든 에너지 상태가 아닌 확정적인 $E$, $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$, $s_z$ 값을 나타내는 에너지 상태만을 다룰 것입니다. 이를 유념하여 정리하자면

수소꼴 원자의 에너지 상태는 다음 observable로 완전히 특정됩니다.

\[E,\: \left| \bold{l} \right|^2,\: l_z,\: \left| \bold{s} \right|^2,\: \text{and}\: s_z\]

따라서 $\psi$를 함수식인 $(\frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \alpha(\sigma))$로 지칭하는 대신 $E$, $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$, $s_z$의 observable만으로 지칭할 수 있습니다. 이 observable의 집합은 이러한 특별한 특성으로 인해 특별한 이름이 있습니다: Complete Set of Commuting Observables (CSCO).

다만 한 에너지 상태를 지칭할 때 5개의 observables의 정확한 값을 매번 제시하는 것은 번거로우며, 따라서 이런 observables 대신 관련된 양자수($n, l, m_l, s, m_s$)를 나열하는 것이 더 편리합니다. 이제는 에너지 상태를 지칭할 때 5개의 양자수를 나타내면 됩니다.

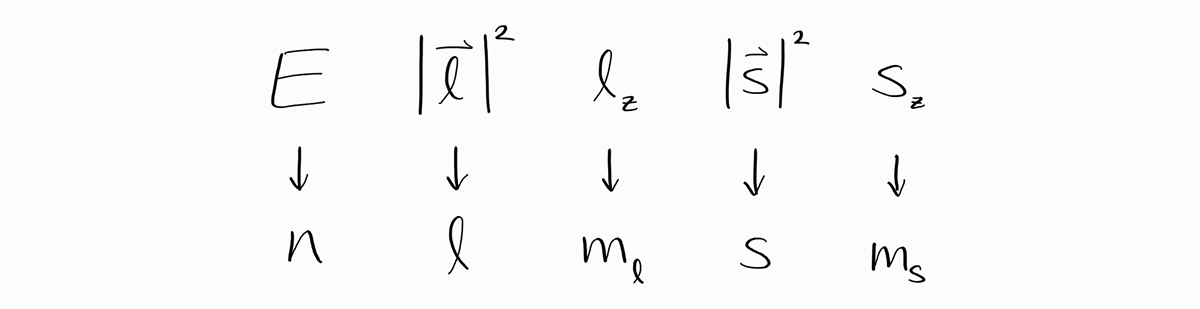
이 양자수는 $\psi$의 유도과정에서 자연스럽게 파생되며, $\psi$에 부과된 경계조건에 의해 정수 또는 반정수(half-integer) 값을 가집니다.

아래는 각 observable과 대응하는 양자수의 관계식을 SI 단위로 나타낸 것입니다.

\[\hat{H} \psi = E \psi = -\frac{Z^2m_ee^4}{8\epsilon_0^2h^2n^2} \psi\] \[\hat{l}^2 \psi = \left| \bold{l} \right|^2 \psi =l\left(l+1\right)\hbar^2 \psi\] \[\hat{l}_z \psi = l_z \psi = m_h \hbar \, \psi\] \[\hat{s}^2 \psi = \left| \bold{s} \right|^2 \psi =s\left(s+1\right)\hbar^2 \psi\] \[\hat{s}_z \psi = s_z \psi = m_s \hbar \, \psi\]

특정 $\psi$를 지칭할 때 $E$는 아래의 식을 활용하여 주양자수 $n = 1,\, 2,\, 3,\, \cdots$으로 치환할 수 있습니다.

\[E = -\frac{Z^2m_ee^4}{8\epsilon_0^2h^2n^2}\]

$\left| \bold{l} \right|^2$는 (궤도) 각운동량 양자수 $l = 0, \,1, \,2, \,\cdots,\, n$로 치환할 수 있습니다.

\[\left| \bold{l} \right|^2=l\left(l+1\right)\hbar^2\]

$l_z$는 자기양자수 $m_l = -l,\, -l+1,\, \cdots, \,0, \,\cdots, \,+l-1, \,+l$로 치환할 수 있습니다.

\[l_z = m_h \hbar\]

$\left| \bold{s} \right|^2$는 $s$라는 양자수로 치환할 수 있습니다.

\[\left| \bold{s} \right|^2 =s\left(s+1\right)\hbar^2\]

수소꼴 원자는 전자가 오직 하나이므로 $s=1/2$입니다. $s$는 모든 수소꼴 원자에서 같기에 에너지 상태를 특정하는데 유용하지 않아 일반화학에서는 생략되곤 합니다. 이 글에서는 $s$를 특별히 생략하지 않으며 이는 더 복잡한 다전자 원자의 스핀을 다루기 위해 대비하는 차원으로 소개하기 위함입니다.

마지막으로 $s_z$는 스핀 (자기) 양자수 $m_s$로 치환할 수 있습니다.

\[s_z = m_s \hbar\]

$m_l$과 같이 $m_s = -s,\, -s+1,\, \cdots, \,+s-1, \,+s$입니다. $s = 1/2$이므로 수소꼴 원자의 경우 $m_s$는 $+1/2$(스핀 업) 또는 $-1/2$(스핀 다운)만 가능합니다.

조금 전 다루었던 $1s$ 오비탈, 스핀 업 에너지 상태는 정확한 함수꼴($(\frac{Z^\frac{3}{2}}{\sqrt{\pi}}e^{-Zr} \alpha(\sigma))$)이나 $E$, $\left| \bold{l} \right|^2$, $l_z$, $\left| \bold{s} \right|^2$, $s_z$의 complete set of commuting observables로 특정할 수 있었습니다. 이번에는 더욱 간편하게 양자수의 모임($\left(n, l, m_l, s, m_s\right) = (1, 0, 0, 1/2, +1/2)$)으로 같은 에너지 상태를 특정할 수 있습니다.

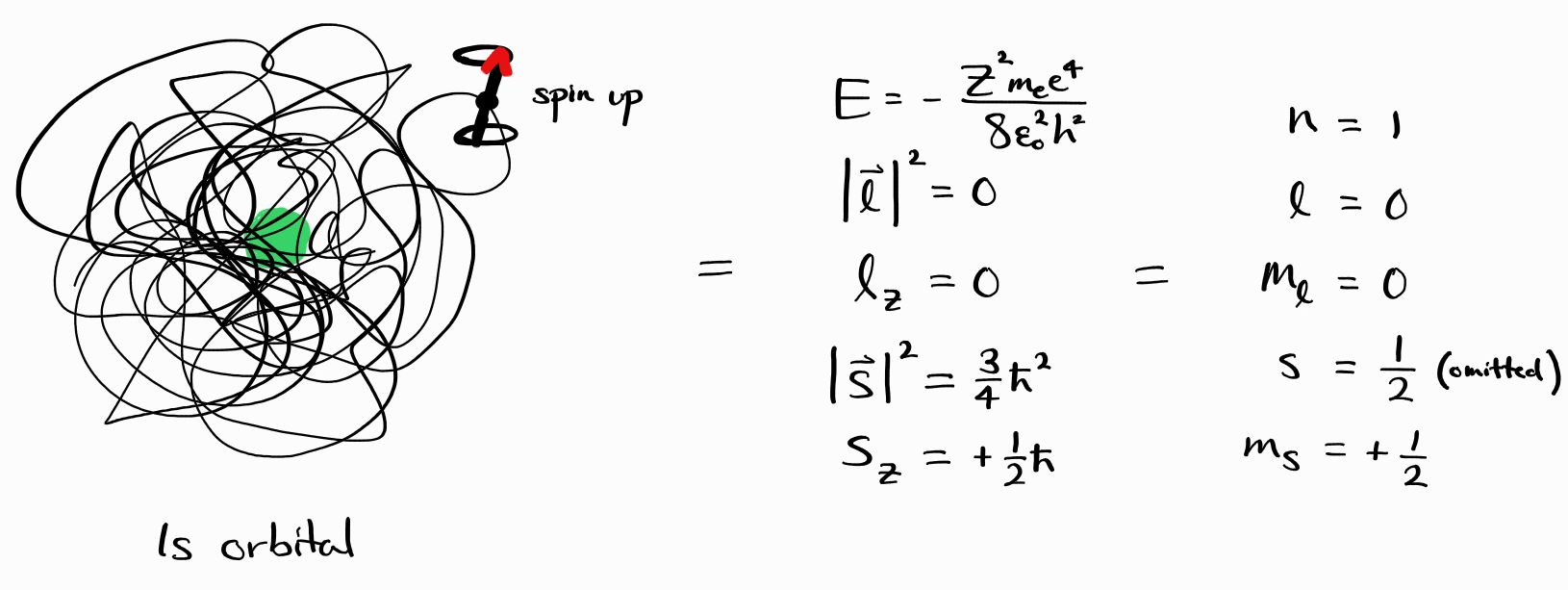
이때 유용한 표기법은 바로 브라켓(bra-ket) 표기법입니다. 이는 벡터(파동함수)를 브라(bra, $|$)와 켓(ket, $ \rangle $)으로 표기하는 것이며, 그 사이에는 벡터의 이름이 들어가게 됩니다. 에너지 상태를 나타내기 위한 가장 적합한 이름은 바로 양자수를 나열한 것($n\,l\,m_l\,s\,m_s$)이며, 아래와 같이 $\psi$를 간단하게 표기할 수 있습니다.

\[\psi = \psi_{\left(n, \,l, \,m_l,\, s,\, m_s\right)} = \left |\, n\,l\,m_l\,s\,m_s\,\right \rangle\]

이에 입각하여 $1s$ 오비탈, 스핀 업 에너지 상태 $\psi$는 $\left |\, 1\,0\,0\,\frac{1}{2}\,+\frac{1}{2}\,\right \rangle$로 표기합니다.

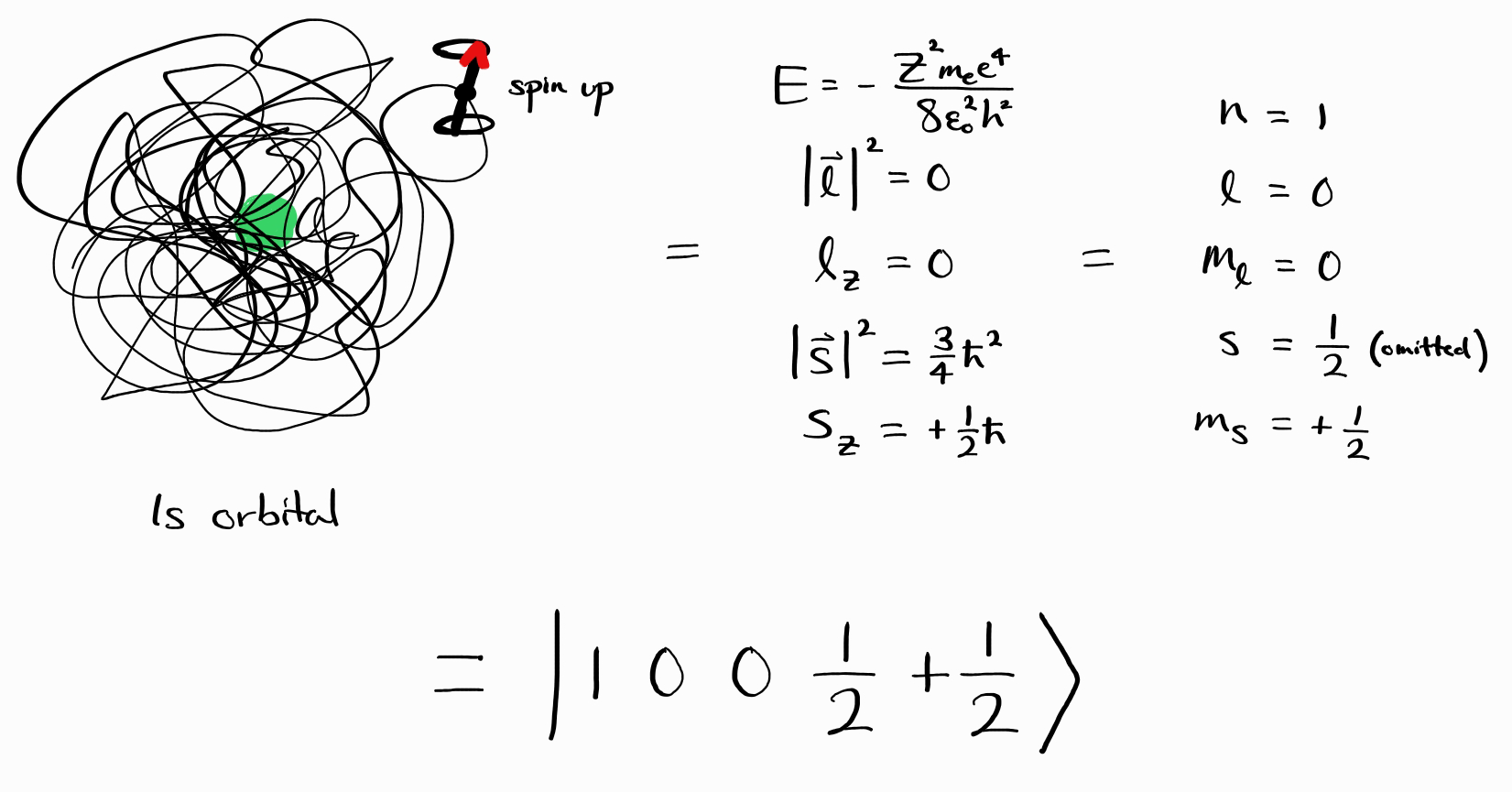
여태까지의 내용은 아래와 같이 정리할 수 있습니다:

수소꼴 원자의 에너지 상태는 궤도 및 스핀 양자수로 특정할 수 있습니다. 브라켓 표기법으로는:

\[\psi = \left |\, n\,l\,m_l\,s\,m_s\,\right \rangle\]

다전자 원자

이쯤 되면 모두가 희망하는 것은 다전자 원자의 에너지 상태가 수소꼴 원자와 비슷한 양자수로 결정되는 것입니다.

단순한 추측을 하자면 에너지 상태가 각각의 전자에 대한 양자수로 결정되지 않을까 싶습니다. 예를 들어 중성 헬륨 원자의 경우 $ \left |\, n_1\,l_1\,m_{l1}\,s_1\,m_{s1};\,n_2\,l_2\,m_{l2}\,s_2\,m_{s2}\,\right \rangle$로 표기되지 않을까 생각할 수 있습니다. 바닥 상태 헬륨은 $ \left |\, 1\,0\,0\,\frac{1}{2}\,+\frac{1}{2};\,1\,0\,0\,\frac{1}{2}\,-\frac{1}{2}\,\right \rangle$이지 않을까요?

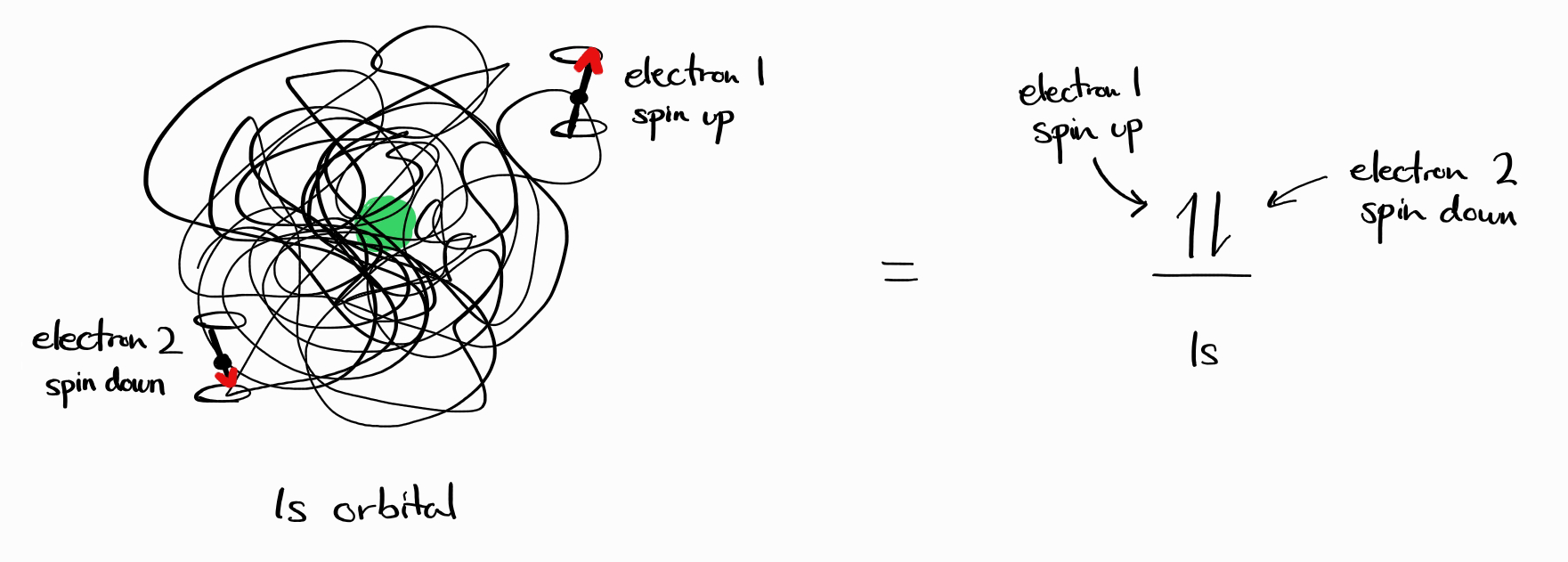
이것이 너무 편리하다고 느끼신다면 직감이 탁월하십니다. 위 추측은 틀렸기 때문이지요. 총 두 개의 상호보완적인 이유로 인하여 에너지 상태는 전자 각각의 양자수로 나타낼 수 없습니다.

우선 수소꼴 원자를 되돌아보면 에너지 상태가 양자수로 나타내지기 위해서는 그 양자수/observable과 연관된 연산자가 Hamiltonian $\hat{H}$와 commute하는 것이 필요조건입니다.

따라서 헬륨 원자가 $ \left |\, n_1\,l_1\,m_{l1}\,s_1\,m_{s1};\,n_2\,l_2\,m_{l2}\,s_2\,m_{s2}\,\right \rangle$로 표기되기 위해서는 연산자 $ \hat{H} _{1} $, $ \hat{l} _{1} ^{2} $, $ \hat{l} _{1z} $, $ \hat{s} _{1} ^{2} $, $ \hat{s} _{1z} $, $ \hat{H} _{2} $, $\hat{l} _2 ^2$, $\hat{l} _{2z}$, $\hat{s} _2 ^2$, $\hat{s} _{2z}$가 $\hat{H}$와 commute해야 합니다. $\hat{H} _1$와 $\hat{H} _2$⁴를 무시하더라도 $\hat{l} _1 ^2$, $\hat{l} _{1z} $, $\hat{s} _1 ^2$, $\hat{s} _{1z} $, $\hat{l}_2 ^2 $, $\hat{l} _{2z} $, $\hat{s} _2 ^2$, $\hat{s} _{2z} $는 $\hat{H}$와 commute하지 않습니다.

이는 헬륨의 에너지 상태가 위에 나열된 모든 연산자의 eigenfunction이 될 수 없기에 확정적인 observable $E$, $\left| \bold{l} _1 \right| ^2$, $l _{1z}$, $\left| \bold{s} _1 \right| ^2$, $s _{1z}$, $\left| \bold{l} _2 \right| ^2$, $l _{2z}$, $\left| \bold{s} _2 \right| ^2$, $s _{2z}$ 값을 가지지 않다는 것을 의미합니다. 따라서 양자수 $l _1\,m _{l1}\,s _1\,m _{s1};\,l _2\,m _{l2}\,s _2\,m _{s2}$를 지정할 수 없게 되며 $ \left |\, n _1\,l _1\,m _{l1}\,s _1\,m _{s1};\,n _2\,l _2\,m _{l2}\,s _2\,m _{s2}\,\right \rangle$와 같은 표기는 불가능합니다.

이에 더불어 $ \left |\, n_1\,l_1\,m_{l1}\,s_1\,m_{s1};\,n_2\,l_2\,m_{l2}\,s_2\,m_{s2}\,\right \rangle$와 같은 표기는 두 전자를 구분할 수 있다는 것을 의미합니다. 하지만 세상의 모든 전자는 같고 서로 구별하는 것이 불가능합니다. 바닥 상태 헬륨의 경우 (1) ‘전자 1’과 ‘전자 2’는 존재하지 않으며 (2) 항상 스핀 업 그리고 항상 스핀 다운인 전자는 없고 어느 전자든 관찰 행위에 의해 스핀 업 또는 다운으로 측정될 수 있습니다.

그렇다면 다전자 원자를 완전하게 명시하는 양자수는 무엇일까요? 다르게 말하자면 어떤 Hamiltonian을 포함한 연산자 모임이 서로 commute하여 complete set of commuting observables를 이룰까요?

먼저 고전역학에서는 각운동량은 벡터량이며 일반적인 벡터처럼 더하고 뺄 수 있습니다. 이를 수식으로 표현하면 아래와 같습니다.

\[\bold{L} = \sum_i \bold{l}_i\]

양자역학에서는 각운동량 연산자가 있으며 이 또한 벡터와 비슷하게 더하고 뺄 수 있습니다. 예를 들어 전체¹ 궤도 각운동량 연산자(total orbital angular momentum operator) $\hat{L}$은 모든 전자의 (궤도) 각운동량 연산자 $\hat{l}_i$의 총합입니다.

\[\hat{L} = \sum_i \hat{l}_i\]

이 연산자 $\hat{L}$은 원자 전체에 대한 궤도 각운동량 연산자입니다. 이로부터 파생된 $\hat{L}^2$과 $\hat{L} _z$는 서로 commute를 할 뿐만 아니라 $\hat{H}$와도 commute합니다. 참고로 $\hat{L} _z$는 $\hat{L}$의 z-성분이며 $\hat{l} _{iz}$는 $\hat{l} _{i}$의 z-성분이기에 아래 관계가 성립합니다.

\[\hat{L}_z = \sum_i \hat{l}_{iz}\]

전체¹ 스핀 연산자 $\hat{S}$는 모든 전자의 스핀 연산자 $\hat{s}_i$의 총합입니다.

\[\hat{S} = \sum_i \hat{s}_i\]

이는 원자 전체의 스핀 연산자입니다. 이로부터 파생된 $\hat{S}^2$과 $\hat{S}_z$는 서로 commute할 뿐만 아니라 $\hat{H}$와도 commute합니다. z-성분에 대하여 위와 같이 아래 관계식도 자연스럽게 성립합니다.

\[\hat{S}_z = \sum_i \hat{s}_{iz}\]

이미 눈치채셨겠지만 두 전체 궤도 각운동량 연산자 ($\hat{L}^2$ 또는 $\hat{L}_z$) 중 하나와 두 전체 스핀 연산자 ($\hat{S}^2$ or $\hat{S}_z$) 중 하나를 고르면 그 두 연산자는 무조건 서로 commute합니다.

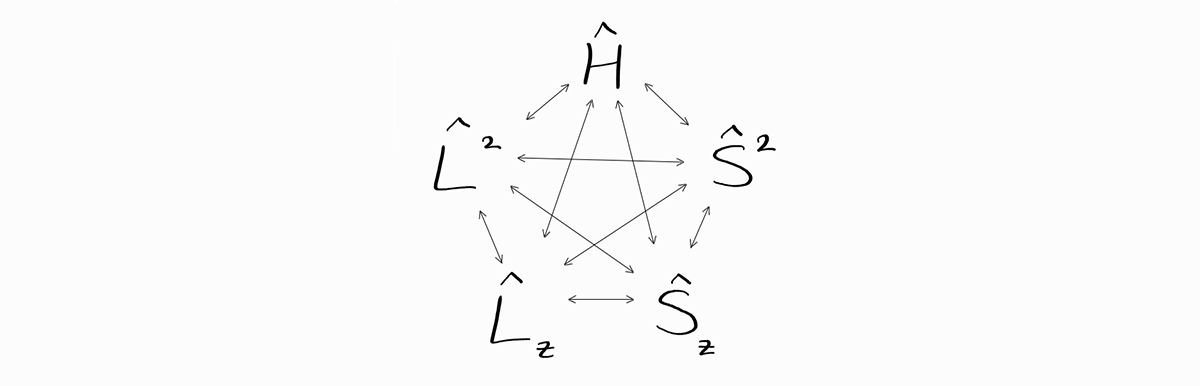
이는 에너지 상태 $\psi \left(r_1, \theta_1, \phi_1, \sigma_1;\,r_2, \theta_2, \phi_2, \sigma_2;\, \cdots ;\,r_n, \theta_n, \phi_n, \sigma_n \right)$가 $\hat{H}$, $\hat{L}^2$, $\hat{L}_z$, $\hat{S}^2$, $\hat{S}_z$ 연산자 모두의 eigenfunction이며 이러한 연산자의 observable로 완전히 특정됨을 의미합니다.

\[\hat{H} \psi = E \psi\] \[\hat{L}^2 \psi = \left| \bold{L} \right|^2 \psi\] \[\hat{L}_z \psi = L_z \psi\] \[\hat{S}^2 \psi = \left| \bold{S} \right|^2 \psi\] \[\hat{S}_z \psi = S_z \psi\]

위의 연산자/observable과 연관된 양자수 중 수소꼴 원자 주양자수 $n$에 대응되는 다전자 원자의 양자수는 특별하기에 맨 마지막에 따로 설명할 예정입니다. 다른 양자수는 수소꼴 원자와 같이 아래의 SI 단위 관계식으로 표현됩니다.

\[\hat{L}^2 \psi = \left| \bold{L} \right|^2 \psi =L\left(L+1\right)\hbar^2 \psi\] \[\hat{L}_z \psi = L_z \psi = M_L \hbar \, \psi\] \[\hat{S}^2 \psi = \left| \bold{S} \right|^2 \psi =S\left(S+1\right)\hbar^2 \psi\] \[\hat{S}_z \psi = S_z \psi = M_S \hbar \, \psi\]

아래의 관계식에 따라 observable $\left| \bold{L} \right|^2$는 전체 궤도 각운동량 양자수 $L = 0, \,1, \,2,\, \cdots$로 대체합니다.

\[\left| \bold{L} \right|^2 =L\left(L+1\right)\hbar^2\]

아래의 관계식에 따라 $L_z$는 $M_L = -L,\, -L+1,\, \cdots, \,+L-1, \,+L$⁵로 대체합니다.

\[L_z = M_L \hbar\]

아래의 관계식에 따라 $\left| \bold{S} \right|^2$는 전체 스핀 각운동량 양자수 $S = 0, \,1/2,\, 1,\, 3/2,\, \cdots$로 대체합니다.

\[\left| \bold{S} \right|^2 =S\left(S+1\right)\hbar^2\]

$S$는 $L$과 다르게 반정수가 될 수 있으며, 수소꼴 원자와 다르게 $1/2$ 이외의 다양한 값이 가능합니다.

아래의 관계식에 따라 $S_z$는 $M_S = -S, \,-S+1, \,\cdots, \,+S-1, \,+S$⁵

\[S_z = M_S \hbar\]

$S$의 값에 따라 $M_S$는 정수이거나 (예를 들어 $S = 1$일 때 $M_S = -1,\, 0,\, +1$) 반정수일 수 있습니다 ($S = 1/2$일 때 $M_S = -1/2, \,+1/2$).

에너지 $E$는 다른 observable과 같이 이산적인 값을 지니지만 양자수를 부여하기 어렵습니다. 그 이유는 양자수와 observable인 $E$를 직접적으로 잇는 관계식이 없기 때문입니다. 따라서 수소꼴 원자와는 다른 방식으로, 양자수를 사용하지 않고 에너지를 특정하는 방법을 강구해야 합니다.

다행히도 대다수의 전자배치의 경우 같은 전자배치의 서로 다른 두 에너지 상태가 동일한 $L$, $M_L$, $S$, $M_S$ 값을 지니지 않습니다. 따라서 대부분의 경우 $E$를 전자배치로 대체할 수 있습니다.

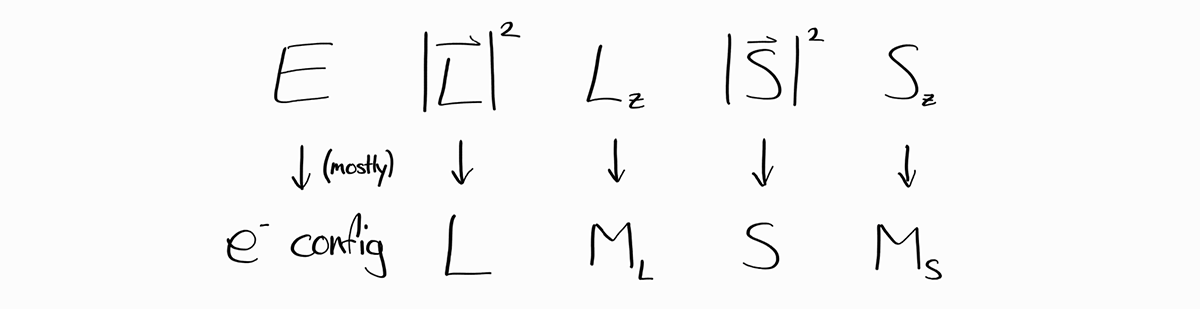
결론적으로 모든 경우에 에너지 상태는 $E$, $L$, $M_L$, $S$, $M_S$로 특정할 수 있으며, 대다수의 경우:

다전자 원자의 에너지 상태는 전자 배치, 궤도와 스핀 양자수로 형용할 수 있습니다. 브라켓 표기로는:

\[\psi = \left |\, (e^- \text{ config)}\,L\,M_L\,S\,M_S\,\right \rangle\]

예를 들어 바닥 상태 헬륨 원자는 $1s^2$, $L=0$, $M_L=0$, $S=0$, $M_S=0$ 이므로(어떻게 이 값을 구하였는지는 나중에 설명할 예정입니다) $\left |\, 1s^2\,0\,0\,0\,0\,\right \rangle$로 표기할 수 있습니다.

각주

1. 이 글은 원자핵의 질량과 운동을 무시하며(고정된 점전하라고 생각합니다) 원자핵의 스핀 또한 무시합니다. 따라서 예시로 주어진 파동함수는 더 정확히 전자의 파동함수라고 지칭해야 합니다. ↩ ↩² ↩³

2. 변수 $\sigma_i$는 $i$번째 전자의 스핀 변수입니다. ↩

3. McQuarrie에서는 수소꼴 원자와 다전자 원자 모두 $\bold{\hat{L}}$, $\hat{L}^2$, $\hat{L}_z$, $\bold{\hat{S}}$, $\hat{S}^2$, $\hat{S}_z$ 표기를 사용합니다. ↩ ↩²

4. 일단 이 두 연산자를 정의하는 것조차 큰 난관입니다. ↩

5. 어떤 이유인지는 모르겠으나 $M_L$과 $M_S$는 특별한 이름이 없으며 $M_L$과 $M_S$로 불립니다. ↩ ↩²