Atomic Term Symbols: 파트 2 - Term Symbol과 Spin-Orbit Coupling
개요
이 글은 원자 term symbol을 소개하고 설명하는 글이며 McQuarrie의 Physical Chemistry: A Molecular Approach 8장을 보충하기 위해 작성되었습니다. 부가적으로 사용된 출처는 Levine의 Quantum Chemistry이며 이해를 위해서는 Physical Chemistry: A Molecular Approach 6장과 7장에 대한 전반적인 이해가 요구됩니다.
이 글에 사용된 표기는 대부분 Physical Chemistry: A Molecular Approach와 일치합니다.
파트 1에서는 양자수가 어떻게 에너지 상태를 특정하는지 배웠으며 이 글에서는 어떻게 term symbol이 에너지 준위를 특정하는지 배울 것입니다. 앞으로 파트 3에서는 더 복잡한 term symbol의 예시 및 훈트 규칙을 다룰 예정입니다.
에너지 상태와 에너지 준위
에너지 상태와 에너지 준위는 양자역학은 물론 물리화학에서도 흔히 사용되는 개념이며, 서로 혼동하여 사용하는 경우 또한 흔합니다. 따라서 아래에 둘의 차이점을 정리해 보았습니다.
에너지 상태는 명확한 에너지를 가지는 파동함수이며 시간 불변 슈뢰딩거 방정식(time-independent Schrödinger equation) $\hat{H}\psi = E\psi$을 만족합니다. 파동함수가 위상을 제외하고는 시간과 상관없이 일정하기에 에너지 상태는 정상 상태(stationary state)라고도 불립니다.
에너지 준위는 시스템이 가질 수 있는 에너지 값입니다. 하나의 에너지 상태가 에너지 준위를 구성할 수 있고, 다르게 여럿의 에너지 상태가 에너지 준위를 구성할 수 있으며 이 경우는 degenerate(축퇴)라고 합니다.
전자 배치 ≠ 에너지 상태 또는 에너지 준위인 이유
일반화학에서는 전자 배치라고 불리는 서로 다른 표기가 있습니다. 아래는 탄소의 바닥 상태 전자 배치를 두 가지 방법으로 나타낸 것입니다.
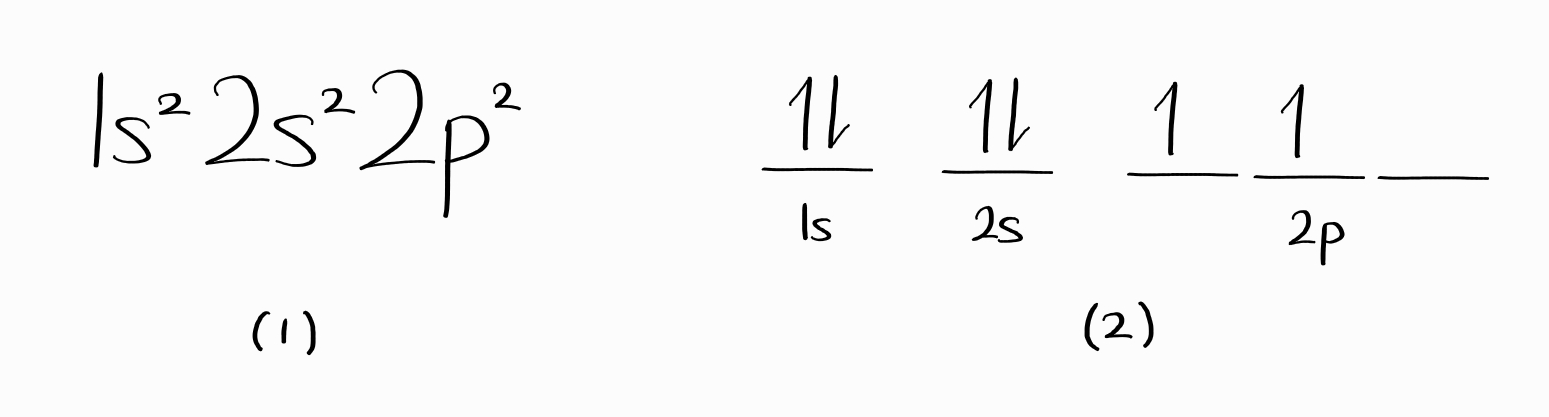
일반적으로 (1) 또는 (2)가 에너지 준위 또는 에너지 상태를 나타낸다고 알려져 있으나 이는 옳지 않습니다.
(1)의 경우 (1)을 만족하는 에너지 상태가 여러 개 있을 수 있으며, 심지어 이 에너지 상태의 에너지 값이 서로 다를 수 있어 하나의 에너지 준위에 대응되지 않습니다.
(2)의 경우 그림에 정확히 입각해서 $\psi$를 세운다면 이 파동함수는 Pauli antisymmetry principle을 따르지 않습니다. 제대로 된 에너지 상태를 나타내려면 이러한 $\psi$ 여럿이 선형 결합해야만 하며, (2) 단독으로는 하나의 에너지 상태를 표현하기 어렵고 이러한 표기 여러 개를 사용해야 합니다.
두 전자 배치의 표기법 모두 에너지 상태나 에너지 준위를 나타내는데 부적절하다는 것을 알 수 있었습니다. 이와 별개로 파트 1에서는 에너지 상태를 아래와 같이 편리하게 표현하는 방법을 보았습니다.
\[\psi = \left |\, (e^- \text{ config)}\,L\,M_L\,S\,M_S\,\right \rangle\]이를 활용하여 파트 2에서는 간단하고 명료하게 원자의 에너지 준위를 나타내는 방법인 atomic term symbols를 배울 것입니다.
Atomic Term Symbol
시작하기 전, 우선 에너지 상태 $\left |\, (e^- \text{ config)}\,L\,M_L\,S\,M_S\,\right \rangle$의 에너지가 어떻게 결정되는지 알아야 합니다. 먼저 에너지를 결정하는 가장 큰 요인은 전자 배치$(e^- \text{ config)$입니다. 두 번째로 주요한 요인은 바로 $S$입니다. 일반화학의 훈트 규칙에서 바닥 상태 전자 배치를 결정할 때 전자 스핀을 최대한 같은 방향으로 만들려 하는 것과 같은 원리이지요. 앞서 언급된 두 요인보다는 덜 중요하지만 $L$ 또한 에너지에 영향을 미칩니다. $L$은 수소꼴 원자의 오비탈 에너지($s = p = d = f = \cdots$)와는 다르게 다전자 원자의 오비탈 에너지가 $l$에 의해 결정되는 것($s < p < d < f < \cdots$)과 관련이 있습니다.
$M_L$과 $M_S$는 에너지에 아무런 영향도 없습니다. 이를 종합적하면 (1) 같은 전자 배치와 (2) 같은 $L$과 (3) 같은 $S$의 에너지 상태는 degenerate하다고 말할 수 있습니다. 이를 에너지 준위 관점으로 정리하여 아래의 결론을 도출할 수 있습니다.
원자의 에너지 준위는 전자 배치, 합계 궤도 각운동량 양자수 $L$, 그리고 합계 스핀 양자수 $S$에 의해 결정됩니다.
에너지 준위를 표기하기 위해서 atomic term symbol1을 도입할 차례입니다. Term symbol은 아래와 같이 $L$과 $S$로 구성되어 있습니다.
\[^{2S+1}L\]여기에서 $L$은 숫자로 표기하지 않고 원자 오비탈과 비슷한 알파벳 문자를 사용합니다.
| $L \,=$ | 0 | 1 | 2 | 3 | 4 | 5 | $\cdots$ |
|---|---|---|---|---|---|---|---|
| $S$ | $P$ | $D$ | $F$ | $G$ | $H$ | $\cdots$ |
Term symbol에서는 직접적으로 $S$를 표기하는 대신 더 유용한 spin multiplicity(스핀 다중도)인 $2S+1$을 표기합니다. $M_S = -S, \,-S+1,\, \cdots ,\,+S-1,\,+S$이기 때문에 가능한 총 $M_S$의 개수가 spin multiplicity $2S+1$이며, 이는 스핀으로 인한 degeneracy입니다. 참고로 한 $L$에 대하여 $M_L = -L, \,-L+1,\, \cdots ,\,+L-1,\,+L$이며 $2L+1$ 가짓수의 $M_L$이 가능하며, 이는 궤도 각운동량으로 인한 degeneracy입니다.
따라서
원자 에너지 준위의 degeneracy는 다음과 같습니다.
\[\left(2L+1\right)\left(2S+1\right)\]
몇 가지 예시를 통하여 term symbol을 이해해봅시다. 수소의 바닥 상태 준위는 $1s^1 : ^2S$입니다. 이는 $S = 1/2$ ($2S+1 = 2$이기에)과 $L = 0$를 의미합니다. 이 바닥 생태 준위의 에너지 상태의 $M_L = 0$ 그리고 $M_S = +1/2, -1/2$이 가능합니다. 위 에너지 상태를 브라켓 표기법으로 나타내면 $\left |\, 1s^1\,0\,0\,\frac{1}{2}\,+\frac{1}{2}\,\right \rangle$과 $\left |\, 1s^1\,0\,0\,\frac{1}{2}\,-\frac{1}{2}\,\right \rangle$이며 둘 다 $1s^1 : ^2S$에 속합니다. 이 에너지 준위의 degeneracy(축퇴도)는 2이며, 이는 간단하게 보고 알거나 spin multiplicity인 $2S+1$를 $2L+1$과 곱하여 알 수 있습니다.
참고로 $^2S$ term symbol은 “doublet S” 또는 “이중항 S”라고 읽습니다.
| $S$ | Spin Multiplicity: $2S+1$ | 명칭 |
|---|---|---|
| $0$ | $1$ | Singlet (단일항) |
| $\frac{1}{2}$ | $2$ | Doublet (이중항) |
| $1$ | $3$ | Triplet (삼중항) |
| $\frac{3}{2}$ | $4$ | Quartet (사중항) |
| $2$ | $5$ | Quintet (오중항) |
| $\frac{5}{2}$ | $6$ | Sextet (육중항) |
더 복잡한 예시는 $1s^22s^22p^3 : ^3P$(triplet P)인 바닥 상태 에너지 준위 질소입니다. Term symbol에 의하면 $L=1$이고 $S=1$입니다. 따라서 이 에너지 준위의 degeneracy는 $(2\times1+1)(2\times1+1) = 9$이며, 질소는 바닥 상태가 총 9개가 있음을 알 수 있습니다.
$L$과 $S$ 구하기: $1s^1 2s^1$
Term symbol을 직접적으로 구하는 첫 번째 예시로 $1s^1 2s^1$ 전자 배치인 들뜬 상태 헬륨을 다루어 봅시다. Term symbol(즉, 에너지 준위)을 구하는 가장 직관적인 방법은 먼저 모든 파동함수(즉, 에너지 상태)를 먼저 찾은 후 이를 에너지 준위/term symbol로 분류하는 것입니다. 이때 필요한 $L$과 $S$는 각 파동함수/에너지 상태를 $\left |\, (e^- \text{ config)}\,L\,M_L\,S\,M_S\,\right \rangle$ 꼴로 정리하면서 자연스럽게 구할 수 있습니다.
따라서 먼저 할 일은 $1s^1 2s^1$ 전자 배치의 파동함수(더 엄밀히 spin orbital(스핀 궤도))를 구하는 것입니다.
첫 번째 접근 방법: 노가다
파동함수가 특별히 전자의 파동함수라면 두 전자의 표지를 서로 바꾸었을 때 전체 파동함수의 부호가 반대로 변해야 하며, 이를 antisymmetric(반대칭)이라고 합니다. 이를 토대로 전자 배치(microstate(미시상태)2라고 불립니다)로부터 파생되는 파동함수를 만들어봅시다.
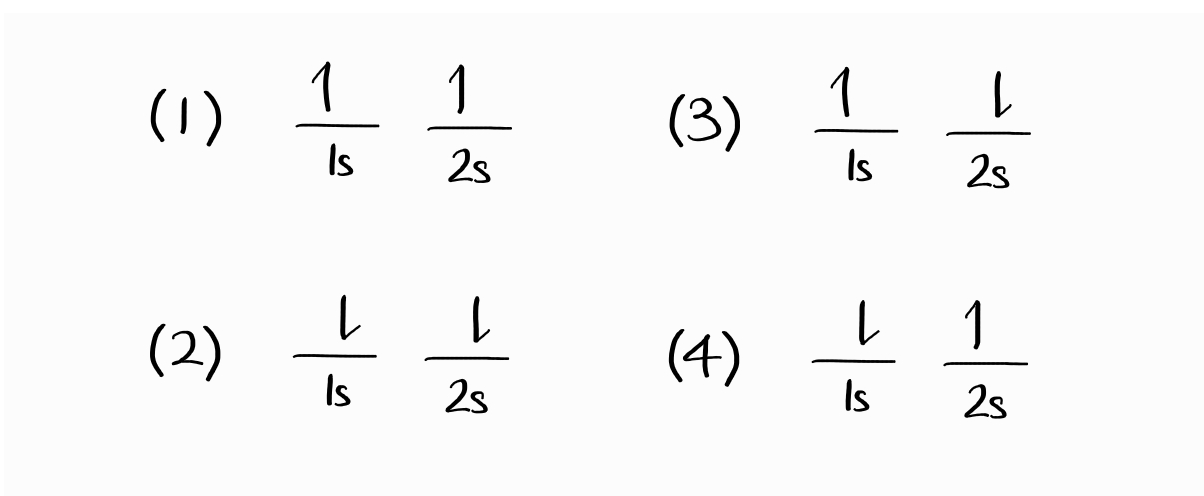
두 전자의 스핀이 업 상태인 첫 번째 microstate에 대응될 법한 파동함수는 $1s(1)\alpha(1)\,2s(2)\alpha(2)$3입니다(이는 전자 1이 $1s$에 스핀 업, 전자 2가 $2s$에 스핀 업 상태로 있다는 것을 의미합니다). 하지만 전자는 서로 구분할 수 없기 때문에 $2s(1)\alpha(1)\,1s(2)\alpha(2)$라는, 이번에는 전자 2가 $2s$에 있는 파동함수도 동등하게 타당한 파동함수입니다.
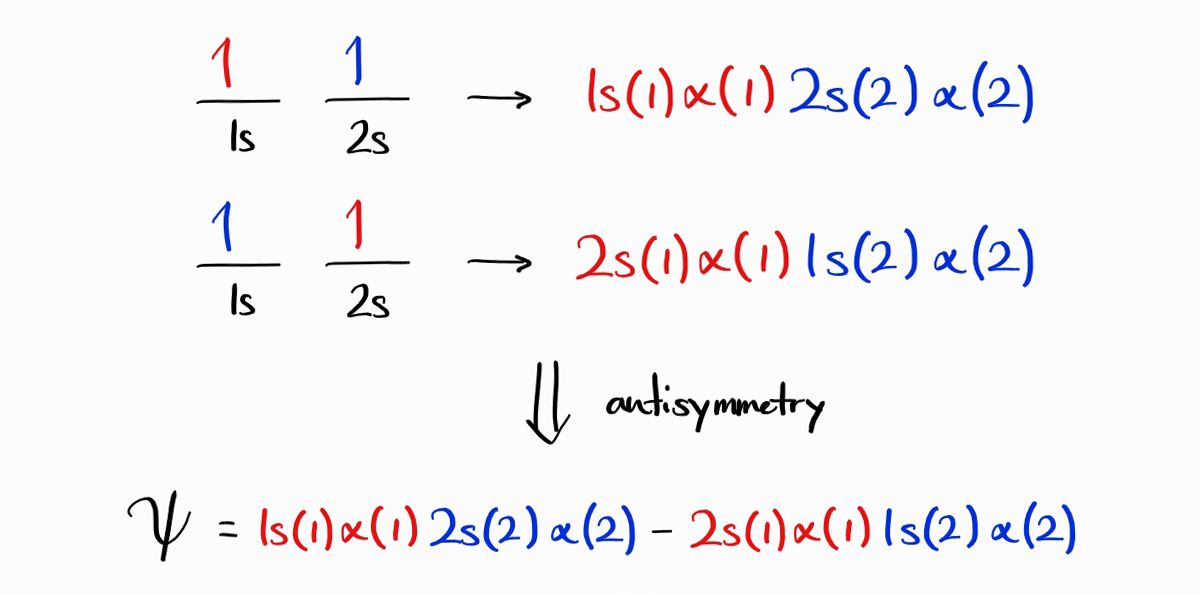
위에서 구한 두 파동함수 $1s(1)\alpha(1)\,2s(2)\alpha(2)$와 $2s(1)\alpha(1)\,1s(2)\alpha(2)$가 전자의 파동함수가 될 수 있을까요? 이 둘은 antisymmetric하지 않기 때문에 전자의 파동함수가 될 수 없습니다. 하지만 흥미롭게도 한 파동함수에서 전자의 표지를 서로 바꾸면 다른 파동함수가 되는 성질을 발견할 수 있습니다. 따라서 위 두 파동함수를 적절히 혼합하여 antisymmetric한 파동함수 $1s(1)\alpha(1)2s(2)\,\alpha(2)-2s(1)\alpha(1)\,1s(2)\alpha(2)$를 만들 수 있습니다. 참고로 Slater determinant를 사용하면 더욱더 쉽게 antisymmetric한 파동함수를 만들 수 있습니다.
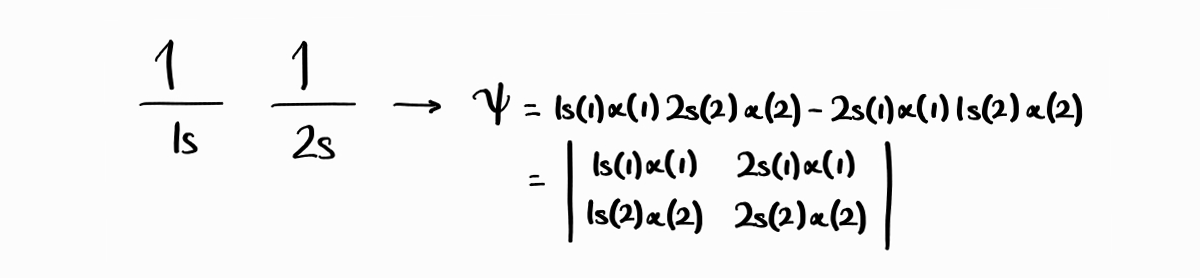
두 번째 microstate는 두 전자의 스핀이 모두 다운 상태이며, 첫 번째 파동함수에서 스핀 업을 모두 다운으로 바꾸어 $1s(1)\beta(1)\,2s(2)\beta(2)-2s(1)\beta(1)\,1s(2)\beta(2)$라는 적합한 파동함수를 만들 수 있습니다.
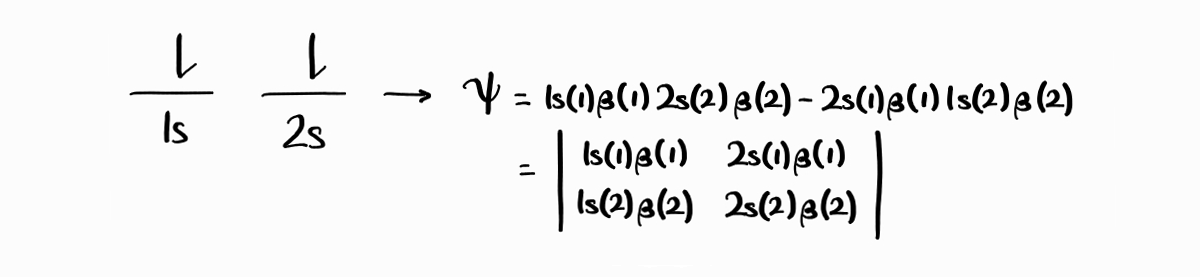
세 번째와 네 번째 microstate는 조금 다릅니다. $1s$ 전자가 스핀 업이고 $2s$ 전자가 스핀 다운인 세 번째 microstate는 우선 $1s(1)\alpha(1)\,2s(2)\beta(2)$와 $2s(1)\beta(1)\,1s(2)\alpha(2)$라는 파동함수를 만들 수 있습니다. $1s$ 전자가 스핀 다운이고 $2s$ 전자가 스핀 업인 네 번째 microstate는 $1s(1)\beta(1)\,2s(2)\alpha(2)$와 $2s(1)\beta(1)\,1s(2)\alpha(2)$라는 파동함수를 만들 수 있습니다.
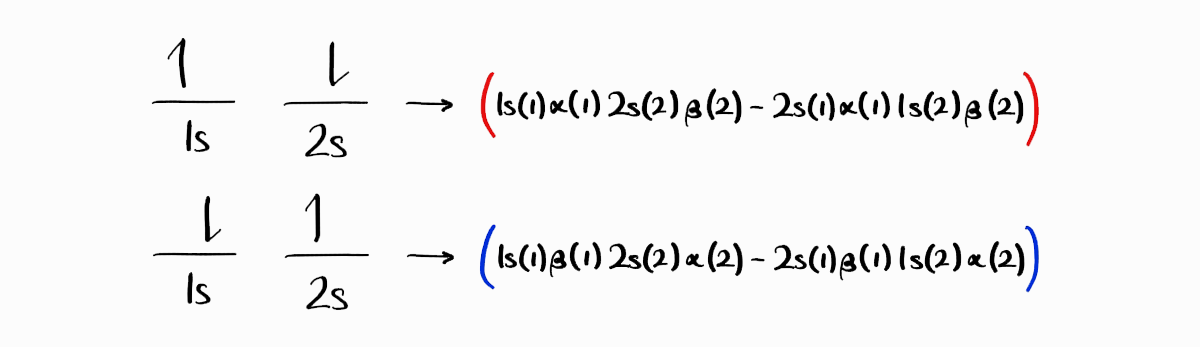
따라서 세 번째 microstate의 antisymmetric한 파동함수가 $1s(1)\alpha(1)\,2s(2)\beta(2) - 2s(1)\beta(1)\,1s(2)\alpha(2)$이고 네 번째 microstate의 antisymmetric한 파동함수가 $1s(1)\beta(1)\,2s(2)\alpha(2)-2s(1)\alpha(1)\,1s(2)\beta(2)$라고 생각하실 수 있으나, 앞의 두 함수는 적합한 파동함수가 아니며 이에는 크게 두 가지 이유가 있습니다.
첫 번째 이유는 전자를 서로 구분하지 못하는 특성입니다. 위에서 보시듯 세 번째 microstate의 $1s$ 전자는 스핀 업, 네 번째 microstate의 $1s$ 전자가 스핀 다운입니다. 하지만 어느 에너지 상태든 한 전자의 스핀이 동등한 확률로 스핀 업이나 스핀 다운이어야 하며, 어느 에너지 상태든 $1s$ 전자가 스핀 업과 스핀 다운 상태의 1:1 선형결합이어야 합니다(이는 $2s$ 전자도 마찬가지입니다). 관점을 달리 보아서 어느 에너지 상태든 한 전자가 속해있는 오비탈이 동등한 확률로 $1s$나 $2s$이어야 하며, 어느 에너지 상태든 스핀 업 전자가 $1s$ 상태와 $2s$ 상태의 1:1 선형결합이어야 합니다(이는 스핀 다운 전자도 마찬가지 입니다). 결론적으로 에너지 상태가 되기 위한 적합한 파동함수를 구하기 위해서는 위에서 구한 두 antisymmetric한 파동함수에 선형결합을 취해야 합니다. 두 파동함수의 덧셈은 한 에너지 상태의 파동함수가 되며(이 또한 antisymmetric합니다), 두 파동함수의 뺄셈은 다른 에너지 상태의 파동함수가 됩니다(또한 antisymmetric).
따라서 $1s(1)\alpha(1)\,2s(2)\beta(2) - 2s(1)\beta(1)\,1s(2)\alpha(2) + 1s(1)\beta(1)\,2s(2)\alpha(2) - 2s(1)\alpha(1)\,1s(2)\beta(2)$와 $1s(1)\alpha(1)\,2s(2)\beta(2) + 2s(1)\beta(1)\,1s(2)\alpha(2) - 1s(1)\beta(1)\,2s(2)\alpha(2) - 2s(1)\alpha(1)\,1s(2)\beta(2)$가 세 번째와 네 번째 에너지 상태의 파동함수입니다.
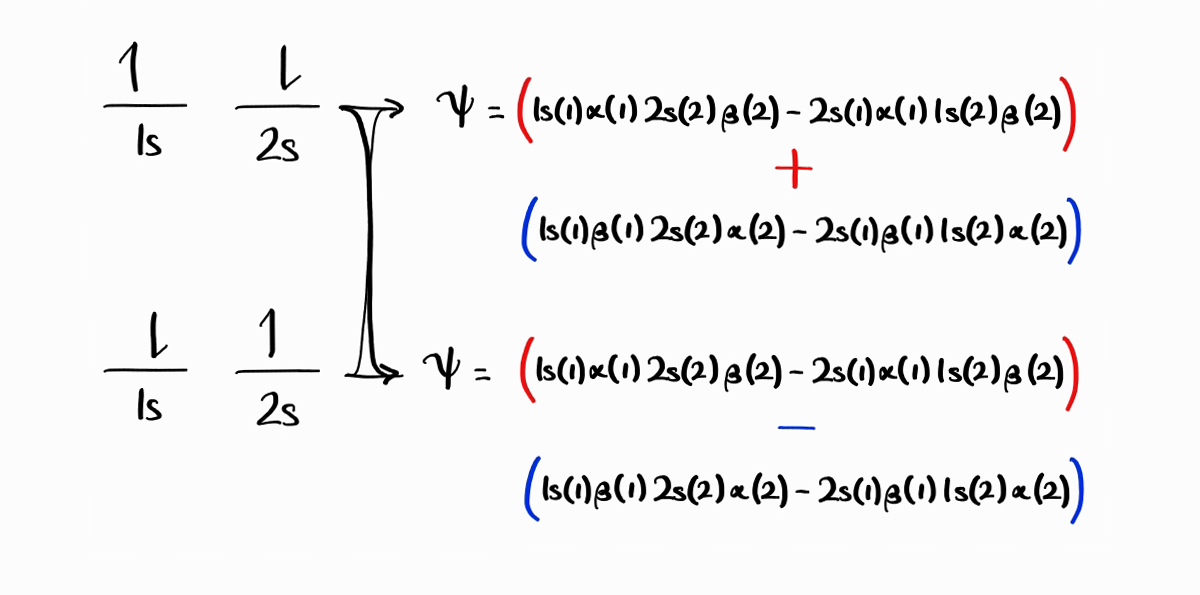
두번째 이유(이유보다는 결론에 비슷하지만)는 새로운 두 antisymmetric 파동함수는 $\hat{H}, \hat{L}^2, \hat{L}_z, \hat{S}^2, \hat{S}_z$의 eigenfunction이지만 처음 만들었던 antisymmetric 파동함수는 아니기 때문입니다.
결과적으로 $1s^12s^1$ 전자 배치로부터 총 4개의 에너지 상태/파동함수를 구할 수 있었습니다. 아래의 파동함수는 $\hat{H}, \hat{L}^2, \hat{L}_z, \hat{S}^2, \hat{S}_z$의 eigenfunction이 되게끔 특별히 선택하였습니다. 여기에서 볼 수 있는 중요한 사실은 에너지 상태/파동함수의 총 개수가 microstate의 총 개수와 같다는 점입니다.
\[1s(1)\alpha(1)\,2s(2)\alpha(2)-2s(1)\alpha(1)\,1s(2)\alpha(2)\] \[1s(1)\beta(1)\,2s(2)\beta(2)-2s(1)\beta(1)\,1s(2)\beta(2)\] \[1s(1)\alpha(1)\,2s(2)\beta(2) - 2s(1)\beta(1)\,1s(2)\alpha(2) + 1s(1)\beta(1)\,2s(2)\alpha(2) - 2s(1)\alpha(1)\,1s(2)\beta(2)\] \[1s(1)\alpha(1)\,2s(2)\beta(2) - 2s(1)\beta(1)\,1s(2)\alpha(2) - 1s(1)\beta(1)\,2s(2)\alpha(2) + 2s(1)\alpha(1)\,1s(2)\beta(2)\]이를 determinant로 표기하면 (Slater determinant를 참고하시기 바랍니다)2:
\[\begin{vmatrix} 1s(1)\alpha(1) & 2s(1)\alpha(1)\\ 1s(2)\alpha(2) & 2s(2)\alpha(2) \end{vmatrix}\] \[\begin{vmatrix} 1s(1)\beta(1) & 2s(1)\beta(1)\\ 1s(2)\beta(2) & 2s(2)\beta(2) \end{vmatrix}\] \[\begin{vmatrix} 1s(1)\alpha(1) & 2s(1)\beta(1)\\ 1s(2)\alpha(2) & 2s(2)\beta(2) \end{vmatrix} + \begin{vmatrix} 1s(1)\beta(1) & 2s(1)\alpha(1)\\ 1s(2)\beta(2) & 2s(2)\alpha(2) \end{vmatrix}\] \[\begin{vmatrix} 1s(1)\alpha(1) & 2s(1)\beta(1)\\ 1s(2)\alpha(2) & 2s(2)\beta(2) \end{vmatrix} - \begin{vmatrix} 1s(1)\beta(1) & 2s(1)\alpha(1)\\ 1s(2)\beta(2) & 2s(2)\alpha(2) \end{vmatrix}\]전자가 2개인 시스템의 경우 공교롭게도 파동함수를 공간 부분 함수와 스핀 부분 함수로 나눌 수 있으며, 이런 인수분해된 꼴은 파동함수의 antisymmetric성이나 다른 특성을 살펴보기에 편리합니다.
\[\left[1s(1)\,2s(2)-2s(1)\,1s(2)\right]\alpha(1)\alpha(2)\] \[\left[1s(1)\,2s(2)-2s(1)\,1s(2)\right]\beta(1)\beta(2)\] \[\left[1s(1)\,2s(2) - 2s(1)\,1s(2)\right]\left[\alpha(1)\,\beta(2) + \beta(1)\,\alpha(2)\right]\] \[\left[1s(1)\,2s(2) + 2s(1)\,1s(2)\right]\left[\alpha(1)\,\beta(2) - \beta(1)\,\alpha(2)\right]\]위 파동함수에 연산자 $\hat{L} ^2 = \left(\hat{l} _1 + \hat{l} _2\right) ^2$, $\hat{L}_z = \hat{l} _{1z} + \hat{l} _{2z}$, $\hat{S} ^2 = \left(\hat{s} _1 + \hat{s} _2\right) ^2$, $\hat{S} _z = \hat{s} _{1z} + \hat{s} _{2z}$를 취하여 $\left|\bold{L}\right| ^2, L_z \left|\bold{S}\right| ^2$, $S_z$를 직접적으로 구해 $L, M_L, S, M_S$를 얻을 수 있습니다. 첫 번째 파동함수의 스핀 부분 함수로 예시를 들자면,
\[\hat{S}_z \left(\alpha(1)\alpha(2)\right) = \left(\hat{s}_{1z} + \hat{s}_{2z}\right)\alpha(1)\alpha(2)\] \[= \hat{s}_{1z}\,\alpha(1)\alpha(2) + \alpha(1)\,\hat{s}_{2z}\,\alpha(2)\] \[= \left(+\frac{1}{2}\hbar\right)\alpha(1)\,\alpha(2) + \alpha(1)\left(+\frac{1}{2}\hbar\right)\alpha(2)\] \[= +\hbar \left(\alpha(1)\alpha(2)\right)\]따라서 $S_z = +\hbar$이고 $M_S = +1$입니다. 위 파동함수의 $M_L$과 $M_S$를 모두 연습 삼아 구하는 것은 연산자에 대한 직관을 형성하는 데 큰 도움이 될 것입니다.
결과는 다음과 같습니다:
| Spatial part | $L$ | $M_L$ | Spin part | $S$ | $M_S$ | Term Symbol |
|---|---|---|---|---|---|---|
| $1s(1)\,2s(2)-2s(1)\,1s(2)$ | 0 | 0 | $\alpha(1)\alpha(2)$ | 1 | +1 | $^3S$ |
| $1s(1)\,2s(2)-2s(1)\,1s(2)$ | 0 | 0 | $\beta(1)\beta(2)$ | 1 | -1 | $^3S$ |
| $1s(1)\,2s(2)-2s(1)\,1s(2)$ | 0 | 0 | $\alpha(1)\,\beta(2) + \beta(1)\,\alpha(2)$ | 1 | 0 | $^3S$ |
| $1s(1)\,2s(2)+2s(1)\,1s(2)$ | 0 | 0 | $\alpha(1)\,\beta(2) - \beta(1)\,\alpha(2)$ | 0 | 0 | $^1S$ |
가능한 $L$과 $S$를 토대로 $^3S$(triply degenerate)와 $^1S$(singly degenerate)가 $1s^12s^1$의 term symbol임을 최종적으로 구할 수 있습니다.
여담이지만 Spin part의 “합”은 (Spatial part를 무시하고) 시각적인 방법으로 나타낼 수 있습니다. 먼저 아래 도식은 스핀 함수 $\alpha$와 $\beta$를 나타낸 것입니다.
이러한 스핀 함수를 곱하고 더해 위의 표에서 볼 수 있는 스핀 부분 함수를 만들어낼 수 있습니다.
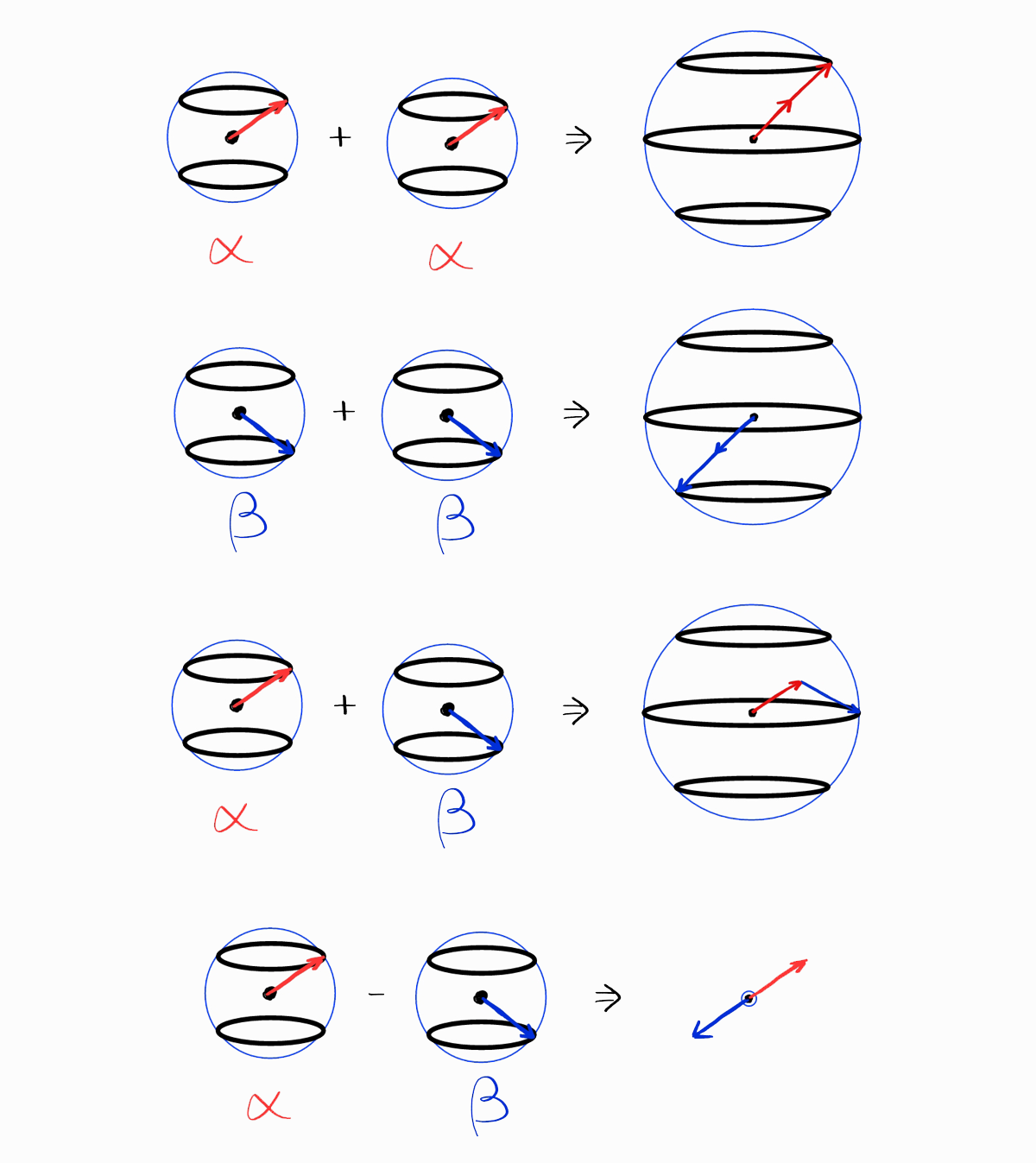
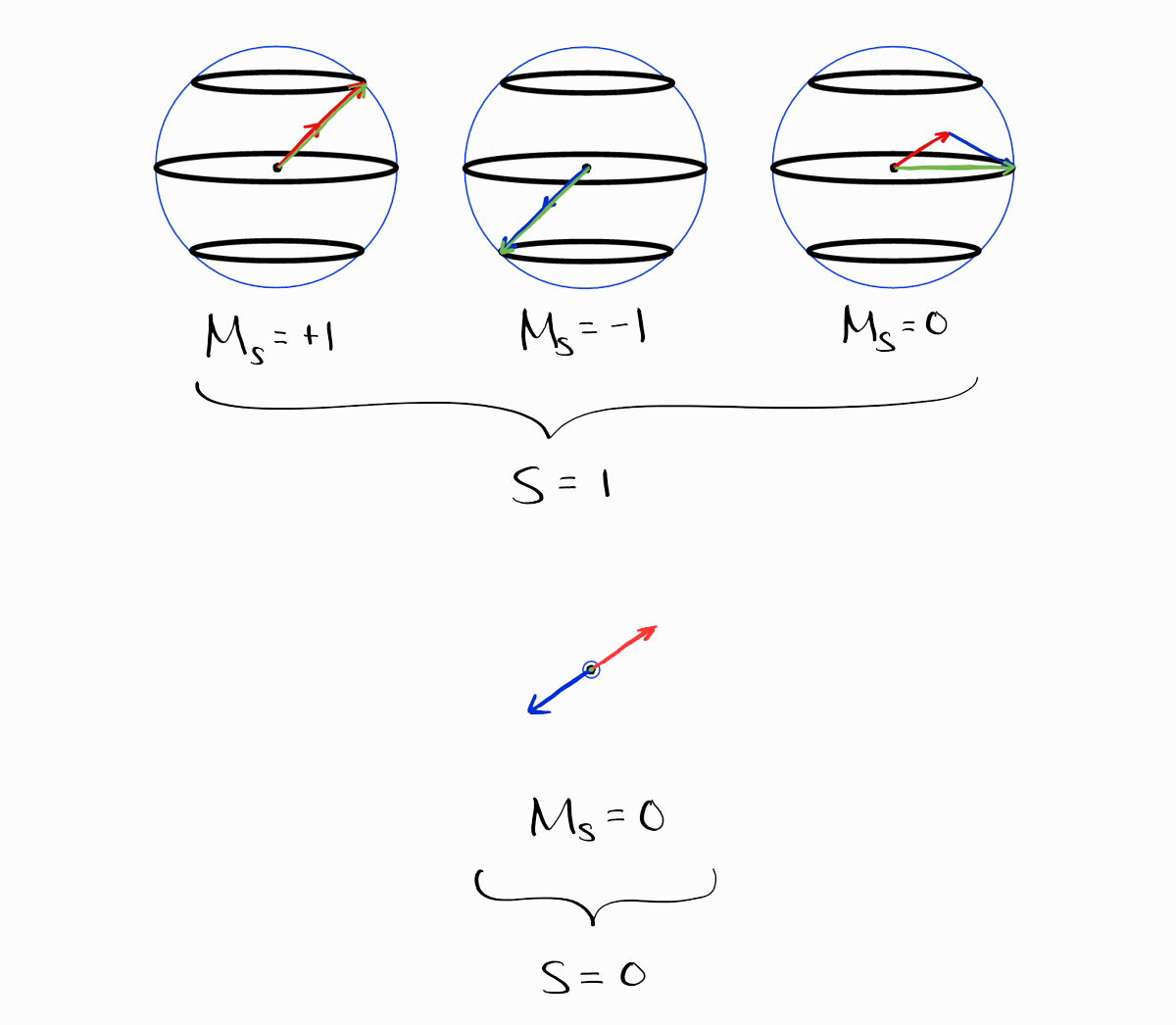
아래의 결과에서 각 스핀 부분의 $S$와 $M_S$가 표의 값과 같음을 알 수 있습니다.
본론으로 돌아가서 접근방식 1의 치명적인 단점은 먼저 모든 파동함수를 일일이 구해야 한다는 점입니다. 파동함수를 구하지 않고 term symbol을 구할 방법이 있을까요?
접근방식 2: microstate에서 $M_L$과 $M_S$ 구하기
위에서 파동함수로부터 $M_L$과 $M_S$를 계산하는 것은 상당히 쉬웠을 것입니다. 이보다 더 쉬운 것은 처음의 microstate로부터 $M_L$과 $M_S$를 구하는 것입니다.
우선 $\hat{S} _z = \hat{s} _{1z} + \hat{s} _{2z}$임을 다시금 기억해내 봅시다. 적당한 eigenfunction에 대해서(위에서 다룬 파동함수 모두가 해당합니다) $S _z = s _{1z} + s _{2z}$가 성립되며 observable이 아닌 양자수의 경우 $M _S = m _{s1} + m _{s2}$임을 알 수 있습니다.
첫 번째 microstate는 두 전자 모두 스핀 업입니다. 따라서 $M_S = +\frac{1}{2}:+\frac{1}{2} = +1$입니다. 두 번째 microstate는 모두 스핀 다운입니다. 따라서 $M_S = -\frac{1}{2}:-\frac{1}{2} = -1$입니다. 세 번째와 네 번째 microstate는 한 전자는 스핀 업, 다른 전자는 스핀 다운이므로 $M_S = 0$입니다.
네 가지 microstate 모두 모든 전자가 $1s$ 오비탈 또는 $2s$ 오비탈에 속해있기 때문에 각 $m_l=0$이며, 따라서 이의 총합인 $M_L = 0$입니다. 이 글에서는 Microstate를 $\left( 0^+, 0^- \right)$처럼 표기할 것인데요, 이는 $m_{l1} = 0, m_{s1} = +1/2, m_{l2} = 0, m_{s2} = -1/2$를 의미합니다.
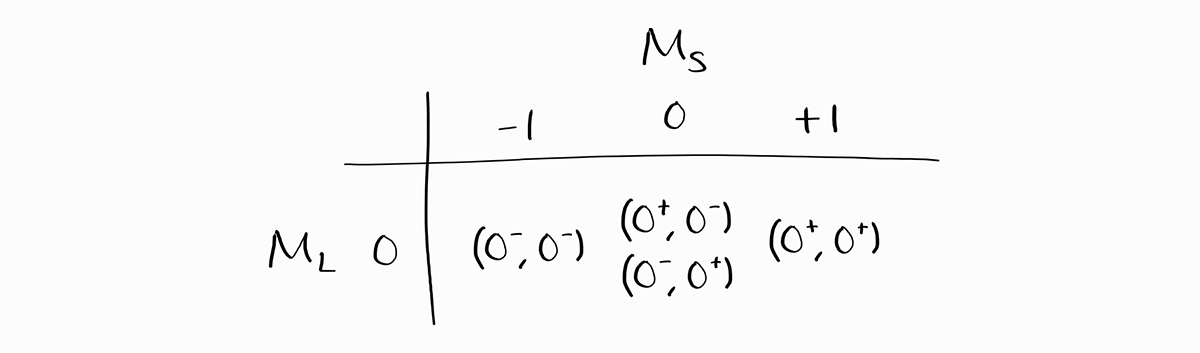
이제 각 term symbol을 구할 때마다 해당하는 microstate(엄밀히 에너지 상태)를 지워 모든 term symbol을 구할 것입니다.
위의 $M_L$과 $M_S$ 값 중 $M_S$의 최댓값은 +1, 최솟값은 -1입니다. 한 term symbol의 $S$의 값이 1보다 크다고 가정해봅시다. 그렇다면 $M_S$의 최댓값은 +1보다 커야 하고, 최솟값은 -1보다 작아야합니다. 그렇지 않으므로 $S$는 1보다 크지 않아야하며 term symbol이 가질 수 있는 최대 $S$는 1임을 결론지을 수 있습니다.
$M_L$의 최댓값은 0이므로 $L$은 무조건 0입니다. 따라서 가능한 최대의 $S$와 최대의 $L$의 조합은 $L = 0$과 $S = 1$입니다. 이는 $^3S$ term symbol에 해당되며 총 3개의 에너지 상태를 포함합니다: $M_L = 0$ 동시에 $M_S = -1, \,0, \,+1$. Term symbol $^3$을 확정 지은 후 위의 표에서 해당하는 $M_L$과 $M_S$에 속한 항 하나씩, 총 3개의 항을 지운 후 더 작은 $S$와 $L$를 지닌 term symbol을 찾습니다.
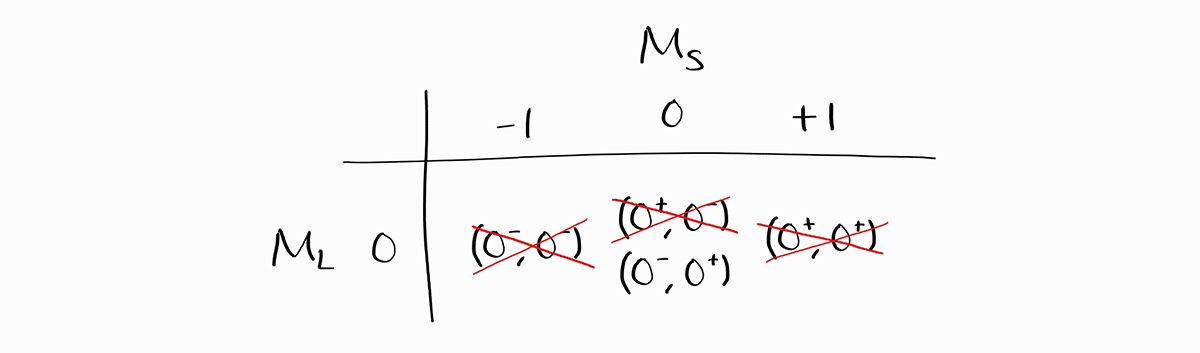
$M_L = 0$과 $M_S = 0$인 항목 중 microstate $\left(0^+, 0^-\right)$을 지우고 $\left(0^-, 0^+\right)$를 지우지 않았습니다. 이는 $^3S$가 $\left(0^+, 0^-\right)$를 포함하고 $\left(0^-, 0^+\right)$는 포함하지 않는다는 것을 의미하지 않으며, 단순히 $M_L = 0$과 $M_S = 0$인 에너지 상태 둘 중 하나가 $^3S$에 포함됨을 의미하며 나머지 에너지 상태는 다른 밝혀지지 않은 term symbol에 포함됨을 의미합니다. 이러한 사실을 가장 엄밀하게 반영해서 지우는 방법은 각 항을 절반씩 지우는 것이겠지만 보는 사람 입장에서 헷갈릴 여지가 있습니다. 따라서 독자의 편의를 위해 microstate 하나를 통째로 지우는 것이며, 어떤 microstate를 지우는지는 전혀 중요하지 않습니다.
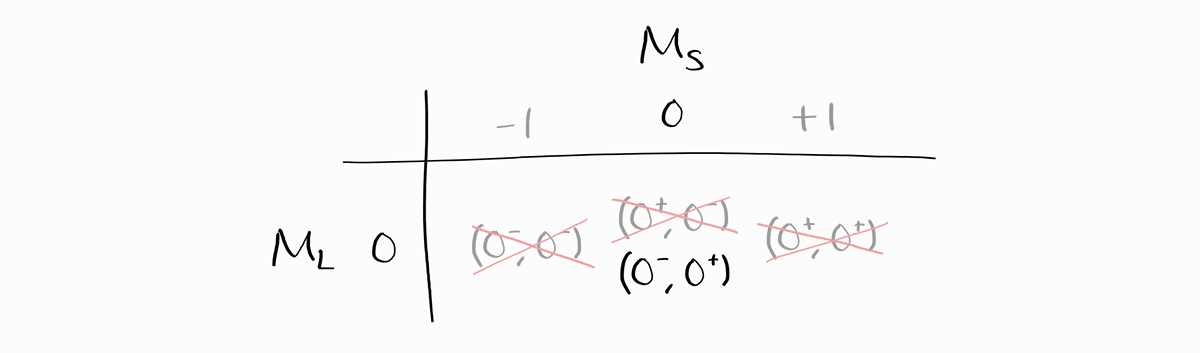
이제 $M_S$의 최댓값은 0이며 $M_L$의 최댓값은 0입니다. 따라서 가능한 $L$과 $S$의 조합은 $L=0$과 $S=0$뿐이며, 이는 $^1S$ term symbol에 해당합니다. 이제 남은 $L = 0$과 $S = 0$에 있는 microstate를 지우고 나면 남은 microstate/에너지 상태가 없게 되며, $1s^12s^1$의 모든 term symbol을 구했다고 말할 수 있습니다.
각운동량의 양자역학적 덧셈
접근방식 2가 접근방식 1보다 월등히 빠르지만 이보다 훨씬 빠르고 간편한 방법이 존재하며, 앞으로 소개할 방법은 접근방식 2를 일반화 한 것입니다. 다시금 되돌아가 $m_{s1}$의 최댓값 $(+\frac{1}{2})$과 $m_{s2}$의 최댓값 $(+\frac{1}{2})$을 더하여 $M_S$의 최댓값 $(+1)$을 구한 것을 떠올려봅시다. $m_{s1}$의 최댓값은 $s_1$이고, $m_{s2}$의 최댓값은 $s_2$이기 때문에 $M_S$의 최댓값은 $s_1 \left(\frac{1}{2}\right)$과 $s_2 \left(\frac{1}{2}\right)$의 합과 같습니다.
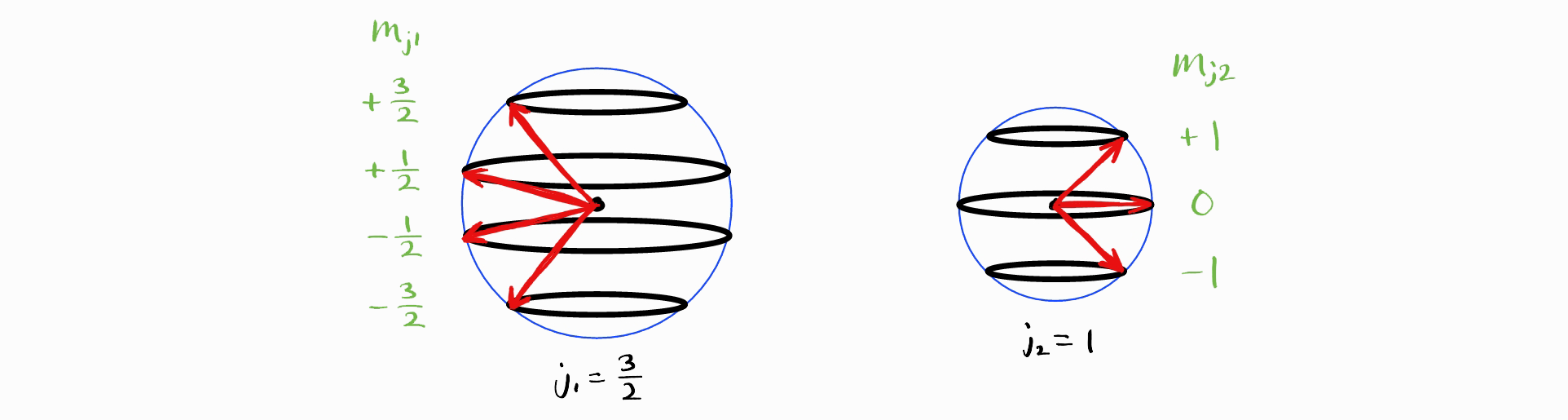
이제는 임의의 각운동량 양자수 $j_1$ and $m_{j1}$과 $j_2$ and $m_{j2}$를 더하여 $J$와 $M_J$ (이에 $j_1$와 $j_2$도 명시하는 것이 엄밀하나 생략하겠습니다) (아래 그림에서는 $j_1 = \frac{3}{2}$이며 $j_2 = 1$입니다).
$M_J$의 최댓값은 $j_1+j_2$입니다.
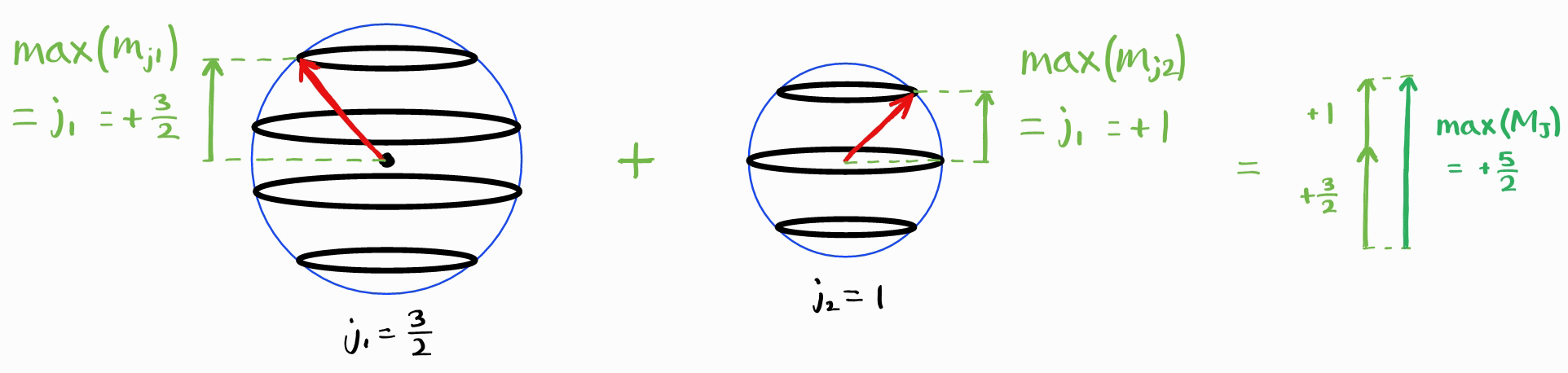
따라서 가능한 $J$의 최댓값은 $j_1+j_2$입니다. 앞서 배운 각운동량 양자수와 동일하게 $M_J$는 $-J, \,-J+1,\,\cdots,\, +J-1, +J$와 같은 값이 가능합니다.
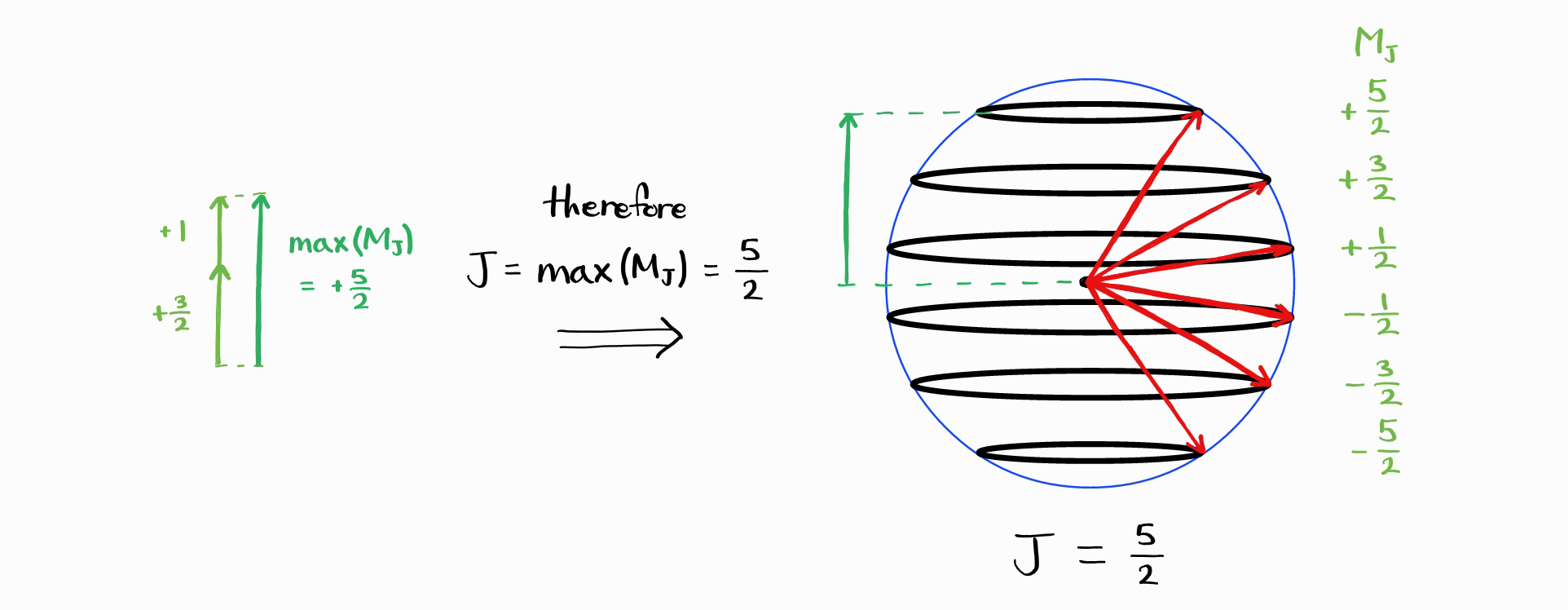
$J_{\text{max}} = j_1 + j_2$임을 알았다면 $J_{\text{min}}$는 무엇일까요? $M_J$의 최솟값은 $m_{j1}$과 $m_{j2}$의 최댓값의 합이 아닌 차입니다. 이는 $j_1$와 $j_2$의 차와 같습니다.
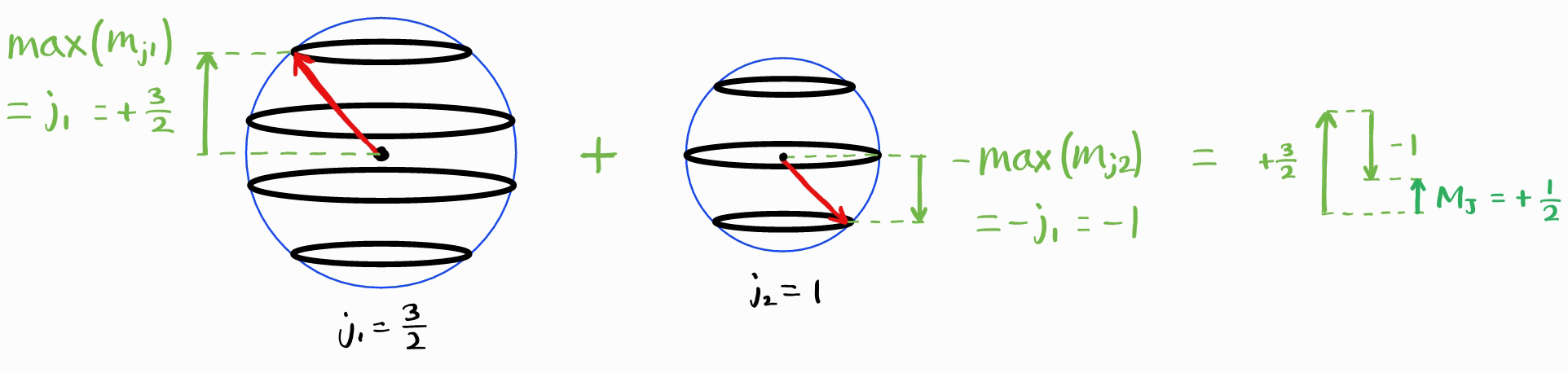
따라서 $M_J$의 최댓값의 최솟값은 $\left|j_1 - j_2\right|$이며, $J$의 최솟값은 $\left|j_1 - j_2\right|$입니다.
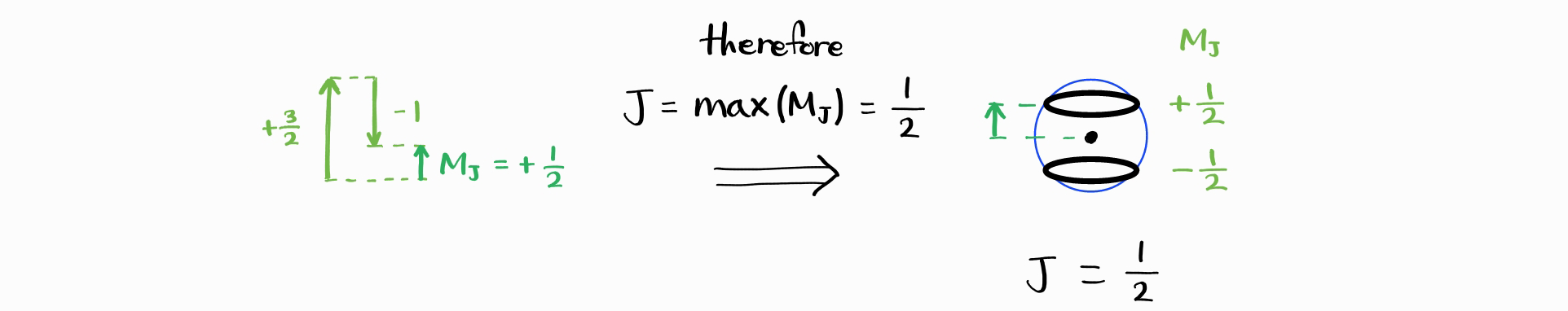
그리하여 $J_{\text{min}} = \left|j_1 - j_2\right|$이며, 가능한 $J$의 값은 $\left|j_1 - j_2\right|,\,\cdots,\,j_1 + j_2$입니다. 확인차 microstate의 총 가짓수(가능한 $j_1$, $m_{j1}$, $j_2$, $m_{j2}$ 조합의 가짓수)와 에너지 상태의 총 가짓수(가능한 $j_1$, $j_2$, $J$, $M_J$ 조합의 가짓수)를 해야려봅시다. $j_1$, $j_2$는 상수이므로 전자는 $\left(2j_1+1\right)\left(2j_2+1\right)$입니다. 후자는 $\sum_J \left(2J+1\right)$를 $J = \left|j_1 - j_2\right|,\,\cdots,\,j_1 + j_2$에 걸쳐 계산한 합입니다.
\[\left(2j_1+1\right)\left(2j_2+1\right) = \sum_{J\,=\,\left|j_1 - j_2\right|}^{j_1 + j_2} \left(2J+1\right)\]수식을 정리해보면 위 등식이 성립함을 보일 수 있습니다. 위 내용을 통틀어 종합하면 아래와 같은 유용한 결론을 지을 수 있습니다.
각운동량 양자수 $j_1$과 $j_2$의 합을 전체 각운동량 양자수 $J$로 표현할 수 있으며 이의 값은 아래와 같다.
\[J=\left|j_1 - j_2\right|,\,\left|j_1 - j_2\right|+1,\,\cdots,\,j_1 + j_2 - 1,\,j_1 + j_2\]
접근 방법 3: 직접적으로 더하기
위의 결론으로 $1s^12s^1$의 $L$과 $S$를 구해봅시다. 먼저 $1s$ 오비탈은 $l_1 = 0$ ($s$ 오비탈)입니다. $2s$ 오비탈은 $l_2 = 0$입니다. 따라서 $L_{\text{min}} = \left| 0 - 0 \right| = 0$이고 $L_{\text{max}} = 0 + 0 = 0$임을 계산할 수 있습니다. 결과적으로 $L = 0$입니다.
스핀의 경우 두 전자 모두 $s = 1/2$입니다. $S_{\text{min}} = \left| 1/2 - 1/2 \right| = 0$이며 $S_{\text{max}} = 1/2 + 1/2 = 1$입니다. 따라서 가능한 $S$는 $0, 1$입니다.
$L = 0$과 $S = 0, 1$를 합쳐 term symbol로 표현하면 $^1S$과 $^3S$입니다. 너무 쉽지 않았나요? 이번 방법은 수많은 경우의 $M_L$과 $M_S$를 직접 세지 않고 바로 term symbol을 구할 수 있는 장점이 있습니다.
하지만 반대로 치명적인 단점도 하나 있습니다. 바로 동일한 부껍질(subshell)에 있는 전자인 equivalent electrons(동등한 전자)에 적용할 수 없다는 점입니다. 예를 들어 $1s^2$에 위 방법을 적용한다면 같은 term symbol이 나올 법합니다. 하지만 파울리 배타 원리에 의하면 두 전자는 서로 같은 스핀일 수 없으며 $M_S = 1$이 불가능하여 기대했던 $S = 1$는 불가능합니다. 대신 두 전자는 서로 다른, 서로 상쇄되는 스핀을 가져 $M_S$는 유일하게 $0$입니다. 따라서 $1s^2$의 term symbol은 유일하게 $^1S$입니다.
간단한 예시로 $1s^12s^13s^1$의 term symbol을 구해봅시다. 이 전자 배치는 $1s^12s^1$와 $3s^1$로 나눌 수 있습니다. $1s^12s^1$는 이미 구했던 예시이며 $l_1 = 0$ & $s_1 = 0, 1$입니다. $3s^1$의 경우 $l_2 = 0$ ($s$ 오비탈) & $s_2 = 1/2$ (전자 1개)입니다.
총 두 가지 경우의 덧셈이 가능합니다: (1) $l_1 = 0$ & $s_1 = 0$과 $l_2 = 0$ & $s_2 = 1/2$ 사이의 덧셈, 또는 (2) $l_1 = 0$ & $s_1 = 1$과 $l_2 = 0$ & $s_2 = 1/2$ 사이의 덧셈입니다. 이를 차례대로 구해봅시다.
(1)의 경우 $l_1 = 0$과 $l_2 = 0$를 더하면 $L_{\text{min}} = \left|0 - 0\right| = 0$이고 $L_{\text{max}} = 0 + 0 = 0$이므로 $L = 0$입니다. 이는 모든 전자가 $s$ 오비탈에 있기 때문에 당연합니다. $s_1 = 0$과 $s_2 = 1/2$를 더하면 $S_{\text{min}} = \left|0 - \frac{1}{2}\right| = \frac{1}{2}$이고 $S_{\text{max}} = 0 + \frac{1}{2} = \frac{1}{2}$입니다. 따라서 $L = 0$, $S = 1/2$이므로 term symbol은 $^2S$입니다.
(2)의 경우 $l_1 = 0$과 $l_2 = 0$의 덧셈의 결과는 (1)과 같이 $L = 0$입니다. $s_1 = 1$에 $s_2 = 1/2$를 더하면 $S_{\text{min}} = \left|1 - \frac{1}{2}\right| = \frac{1}{2}$과 $S_{\text{max}} = 1 + \frac{1}{2} = \frac{3}{2}$입니다. 따라서 $L = 0$, $S = 1/2,\, 3/2$이므로 term symbol은 $^2S$과 $^4S$입니다.
결과적으로 $1s^12s^13s^1$의 term symbol은 $^2S$ (two)와 $^4S$입니다.
Spin-Orbit Coupling (스핀-궤도 결합)
아래의 정리를 기억하시나요?
원자의 에너지 준위는 전자 배치, 전체 궤도 각운동량 양자수 $L$, 그리고 전체 스핀 양자수 $S$에 의해 결정됩니다.
사실 이는 거짓입니다. 알고 보니 spin-orbit interaction (스핀-궤도 상호작용)이라는 양자역학적 효과가 에너지에 정말 미세한 영향을 줍니다. 같은 전자 배치, $L$, $S$를 지닌 에너지 상태는 거의 degenerate하지만 완전히 degenerate하지는 않습니다. 이에 대한 설명을 위하여 처음에 다루었던 Hamiltonian $\hat{H}$으로 돌아가 봅시다.
파트 1에서 다전자 원자의 $\hat{H}$를 원자 단위로 표기하면 다음과 같았습니다.
\[\hat{H} = \hat{H}^{(0)} = \sum_{i\,=\,1}^{n}\left ( -\frac{1}{2}\nabla_i^2 \right ) + \sum_{i\,=\,1}^{n}\left ( -\frac{Z}{r_i} \right ) + \sum_{i}\sum_{j\,>\,i} \left ( \frac{1}{r_{ij}} \right )\]이 Hamiltonian (이상 $\hat{H}^{(0)}$로 표기함)은 다른 연산자 $\hat{L}^2$, $\hat{L}_z$, $\hat{S}^2$, $\hat{S}_z$와 모두 서로 commute하였으며, 이로 인하여 같은 전자 배치, $L$, $S$의 에너지 상태는 degenerate하였습니다. 하지만 실제 Hamiltonian $\hat{H}$는 모든 전자에 대해 $\hat{\bold{l}}_i\cdot\hat{\bold{s}}_i$로 표현되는 항($\hat{H}^{(1)}$)을 포함합니다. 대략적으로 설명하자면 $\hat{\bold{l}}_i\cdot\hat{\bold{s}}_i$는 전자 스핀으로 인한 자기 모멘트와 전자의 궤도에 의한 자기장의 상호작용을 나타낸다고 할 수 있습니다. 따라서 실제 Hamiltonian은 $\hat{H}^{(0)}$보다 다음 식과 더 가깝습니다 (함수 $\xi(r_j)$는 크게 중요하지 않습니다).
\[\hat{H} = \hat{H}^{(0)} + \hat{H}^{(1)} = \sum_{i\,=\,1}^{n}\left ( -\frac{1}{2}\nabla_i^2 \right ) + \sum_{i\,=\,1}^{n}\left ( -\frac{Z}{r_i} \right ) + \sum_{i}\sum_{j\,>\,i} \left ( \frac{1}{r_{ij}} \right ) + \sum_{i\,=\,1}^{n} \left( \xi(r_i)\, \hat{\bold{l}}_i\cdot\hat{\bold{s}}_i \right)\]참고로 원자 번호가 30보다 작은 원소의 경우 $\hat{H}^{(1)}$의 영향이 $\hat{H}^{(0)}$에 비해 무척이나 작습니다. 따라서 $\hat{L}^2$, $\hat{L}_z$, $\hat{S}^2$, $\hat{S}_z$가 $\hat{H}$과 거의 commute하는 것이며 다전자 원자의 경우
\[E^{(1)} \approx \frac{1}{2}A[J(J+1) - L(L+1) - S(S+1)]\]의 미세한 에너지 차이가 발생합니다. 이 0.1% 정도의 사소한 차이로 인해 $L$과 $S$에 따른 degeneracy가 무너지게 됩니다.4
그렇다면 위의 식에서 $J$는 무엇일까요? 먼저 $\bold{J}$는 전체 각운동량을 의미하며 $\bold{L} + \bold{S}$와 같습니다. 이러한 전체 궤도 각운동량 $\bold{L}$과 전체 스핀 각운동량 $\bold{S}$의 결합은 L-S coupling 또는 Russell-Saunders coupling이라고 불립니다. 이를 연산자로 표현하자면
\[\hat{J} = \hat{L} + \hat{S}\]$\hat{L}$과 $\hat{S}$ 같이 $\hat{J}$도 자기만의 양자수($J$와 $M_J$)가 있으며 아래 관계식을 따릅니다 (참고로 $M_J = -J, \,-J+1,\,\cdots,\,+J-1,\,+J$).
\[\hat{J}^2 \psi = \left\| \bold{J} \right\|^2 \psi =J\left(J+1\right)\hbar^2 \psi\] \[\hat{J}_z \psi = J_z \psi = M_J \hbar \, \psi\]이전에는 $\hat{H}$, $\hat{L}^2$, $\hat{L}_z$, $\hat{S}^2$, $\hat{S}_z$가 서로 commute하여 complete set of commuting observables를 이루었습니다. 지금은 $\hat{H}$, $\hat{L}^2$, $\hat{S}^2$, $\hat{J}^2$, $\hat{J}_z$가 서로 commute하여 complete set of commuting observables를 이룹니다.
따라서 에너지 상태를 특정하기 위해서는 $L$, $M_L$, $S$, $M_S$가 아닌 $L$, $S$, $J$, $M_J$를 사용해야합니다. 에너지 준위(즉, term symbol)의 경우 $L$, $S$, $J$를 사용합니다. 다른 $M_J$ 값을 가지지만 같은 $L$, $S$, $J$의 값을 가지는 에너지 상태는 degenerate하기 때문에 $M_J$가 없는 것이며 이는 $E^{(1)}$ 식에 $M_J$가 없다는 사실로부터 유추할 수 있습니다.
그렇다면 $L$과 $S$로부터 $J$를 어떻게 구할 수 있을까요? 궤도 각운동량 양자수 $l_1$과 $l_2$를 서로 “더하거나” 스핀 양자수 $s_1$과 $s_2$를 서로 “더하는” 것처럼 전체 각운동량 양자수 $J$는 $L$과 $S$를 “더하여” 구할 수 있습니다.
특정 $L$과 $S$에 대하여 가능한 전체 각운동량 양자수 $J$는 다음과 같다.
\[J=\left|L - S\right|,\,\left|L - S\right|+1,\,\cdots,\,L + S - 1,\,L + S\]
예를 들어 $L = 1$이고 $S = 1$이라면 $J = 0, 1, 2$가 가능합니다.
이제 에너지 준위를 특정하기 위해서 $L$, $S$, $J$가 모두 필요하므로 term symbol의 표기가 $^{2S+1}L$에서1
\[^{2S+1}L_J\]
로 바뀌게 됩니다.
이 term symbol의 degeneracy는 기존의 $\left(2L+1\right)\left(2S+1\right)$가 아닌 $2J+1$(가능한 $M_J$의 총 개수)입니다.
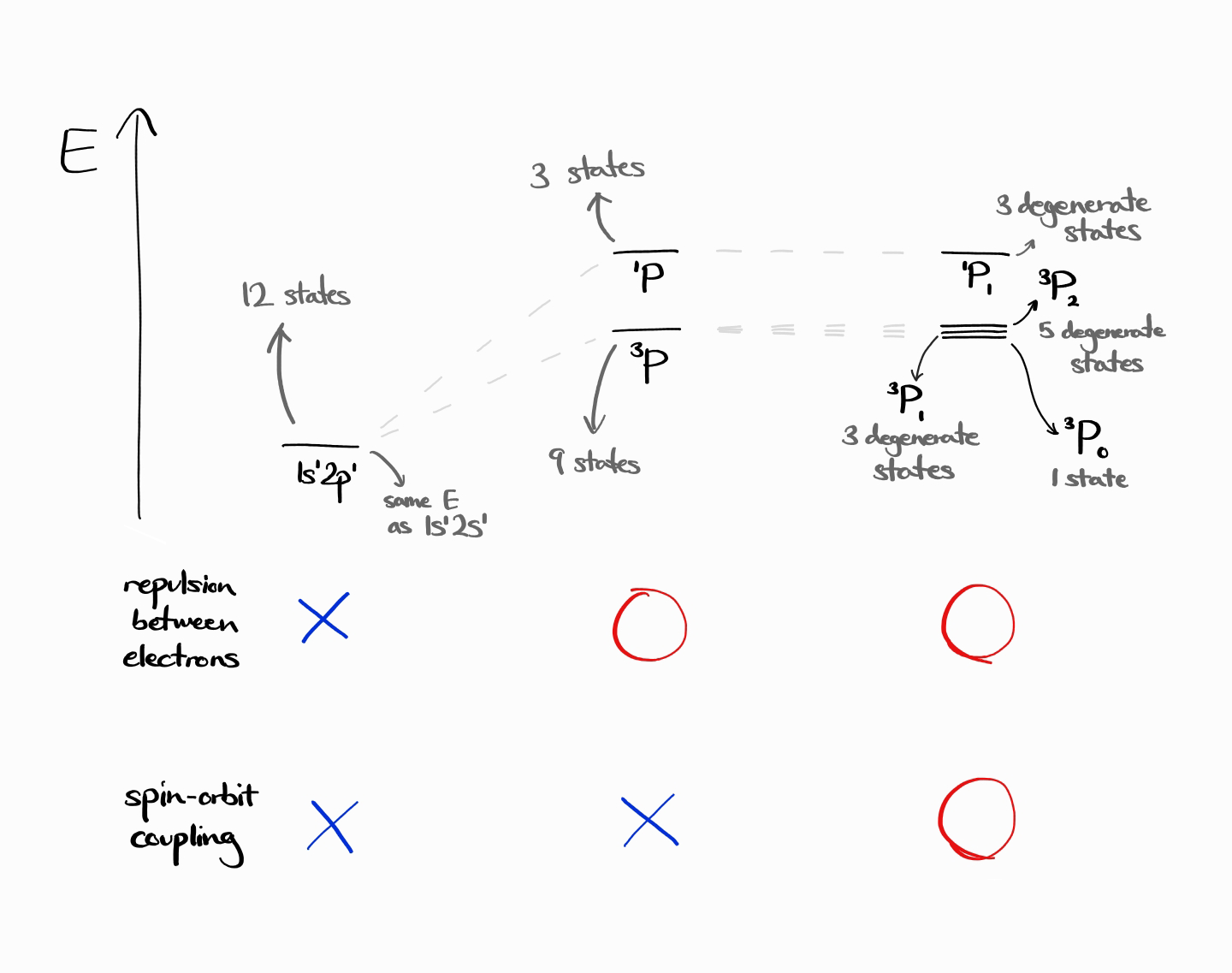
$L = 1$, $S = 1$인 경우 $J = 0, 1, 2$이므로 term symbol은 $^3P$가 아닌 $^3P_0, ^3P_1, ^3P_2$로 분화됩니다. 더 구체적으로 설명하자면 $^3P$의 9개의 degenerate한 에너지 상태는 사실 $^3P_0$의 에너지 상태 1개, $^3P_1$의 degenerate한 에너지 상태 3개, 그리고 $^3P_2$의 degenerate한 에너지 상태 5개였던 것입니다. 보다시피 spin-orbit coupling에 의해 에너지 상태의 개수는 변화하지 않습니다. 따라서 특정 $L$과 $S$ 값에 대하여
\[\left(2L+1\right)\left(2S+1\right) = \sum_{J \, = \, \left| L - S \right|}^{L+S}\left(2J+1\right)\]가 성립합니다.
결론
아래는 여태까지 term symbol에 대하여 배운 것을 정리해보았습니다.
- 에너지 상태의 에너지는 전자 배치와 양자수에 의해 결정되며, 그 양자수는 전체 궤도 각운동량 양자수 $L$, 전체 스핀 양자수 $S$, 그리고 전체 각운동량 양자수 $J$입니다.
- 에너지 준위는 $^{2S+1}L_J$와 같은 atomic term symbol을 통해 나타냅니다.
한 전자 배치의 term symbol을 구하는 방법 중 실용성이 있는 방법은 크게 두 개이며, 이는 접근 방법 2와 3입니다.
접근 방법 3: 동등하지 않은 전자(non-equivalent electrons)만 가능
- 각운동량 양자수의 “덧셈”을 통해 $L$과 $S$를 먼저 구한다.
- $L$과 $S$의 “덧셈”을 통해 $J$를 구한다.
접근 방법 2: 동등한 전자(equivalent electrons)의 경우5
- 모든 microstate를 $M_L$과 $M_S$에 따라 표로 정리합니다. 가장 큰 $S$와 $L$을 가진 term symbol에 해당하는 microstate를 지워나가며 단계적으로 term symbol을 구합니다.
- 모든 term symbol의 $L$과 $S$의 “덧셈”을 통하여 $J$의 term symbol을 구합니다.
간단한 문제로 $1s^12p^1$ 들뜬 상태 헬륨의 term symbol을 직접 구해보는 것 어떤가요?
Term symbol은 $^3P_0$, $^3P_1$, $^3P_2$, $^1P_1$입니다. 아래 도표는 각 term symbol의 에너지를 나타내며, 에너지 준위의 에너지 값과 degeneracy가 Hamiltonian이 변함에 따라 어떻게 변하는지 이해할 수 있습니다.
각주
-
Levine과 같은 일부 서적은 term이 “에너지 준위” (전자 배치, $L$, $S$로만 특정되며 $J$는 고려하지 않은)를 뜻하며, term symbol 은 그 term의 표기를 뜻합니다. 이 경우 term은 촘촘하게 떨어진 에너지 준위의 모임(전자 배치, $L$, $S$, 그리고 $J$에 의해 특정됨)입니다. ↩ ↩2
-
이 표기법이 익숙하지 않으시다면 McQuarrie에서 284페이지를 보시기 바랍니다. 참고로 이 글에서 다루는 모든 파동함수는 정규화가 되어있지 않지만 무조건 정규화가 가능합니다. ↩ ↩2
-
이러한 전자 배치를 microstate(미시상태)라고 부르는 이유는 전체 원자(macrostate(거시상태))를 구성하는 마치 전자를 독립적으로 취급해서 각 전자의 양자수, 즉 상태를 아는 것처럼 나타내었기 때문에 이렇게 불립니다. ↩
-
이에 따라 원자의 스펙트럼에 fine structure(미세구조)가 생기는 것입니다. ↩
-
동등하지 않은 전자(non-equivalent electrons)에도 적용할 수 있습니다. ↩
