Atomic Term Symbols: 파트 3 - 예시 및 훈트 규칙

개요

이 글은 원자 term symbol을 소개하고 설명하는 글이며 McQuarrie의 Physical Chemistry: A Molecular Approach 8장을 보충하기 위해 작성되었습니다. 부가적으로 사용된 출처는 Levine의 Quantum Chemistry이며 이해를 위해서는 Physical Chemistry: A Molecular Approach 6장과 7장에 대한 전반적인 이해가 요구됩니다.

이 글에 사용된 표기는 Physical Chemistry: A Molecular Approach와 대부분 일치합니다.

앞서 파트 1과 2에서는 다전자 원자와 term symbol에 관하여 설명하였습니다. 이번 파트 3에서는 term symbol과 관련한 여러 팁과 훈트 규칙을 다룰 것입니다.

예시: 탄소 $1s^22s^22p^2$

$1s^22s^22p^2$ 탄소에는 총 6개의 전자가 있으며, 이는 여태까지 보았던 예시보다 훨씬 많습니다. 아래는 $1s^22s^22p^2$의 microstate의 예시입니다.

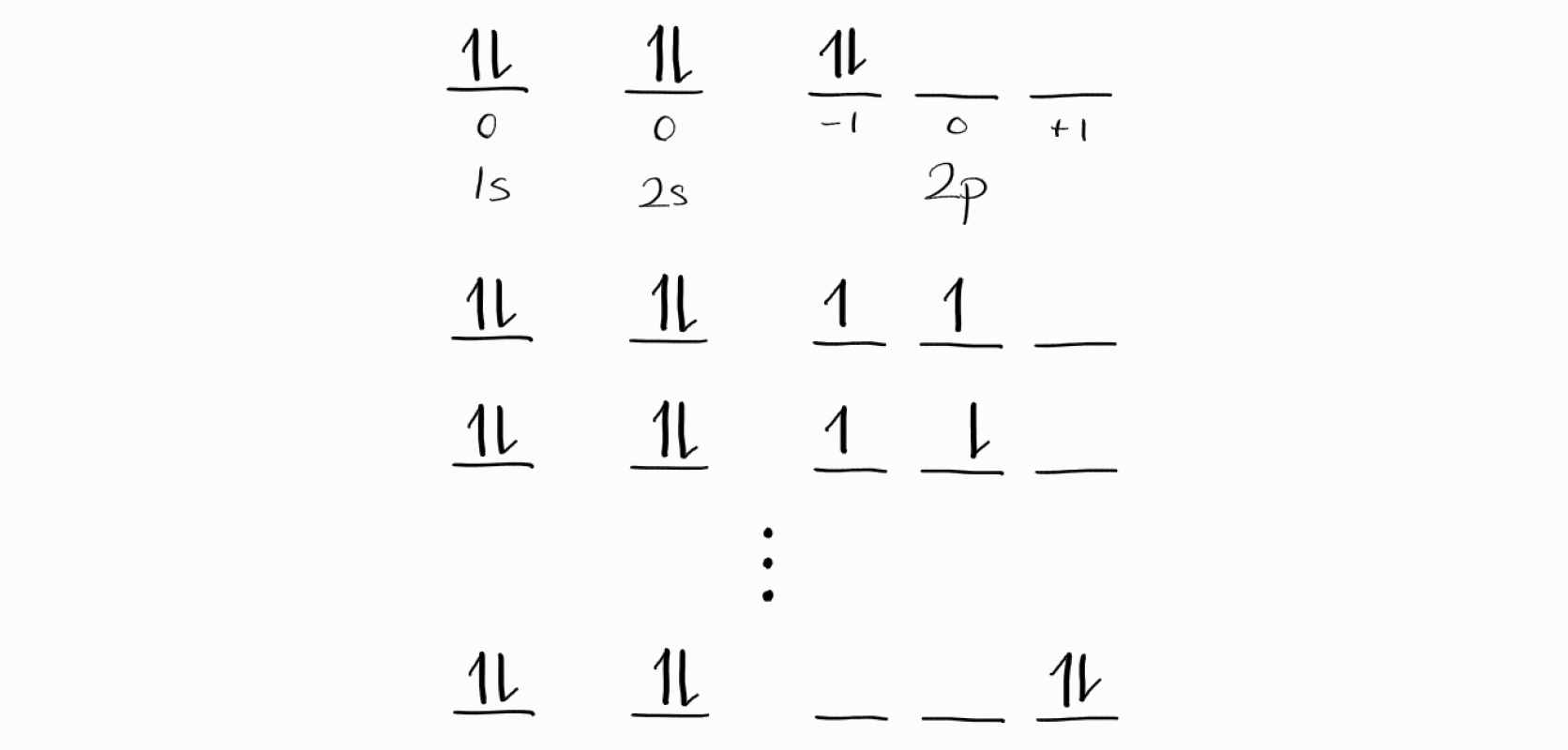
$1s$와 $2s$ 오비탈에 있는 4개의 전자는 모든 microstate에서 동일합니다. 또한 이 4개의 전자는 $M_L = m_{l1} + m_{l2} + \cdots = 0$이고 서로 스핀이 상쇄되기 때문에 $M_S = m_{s1} + m_{s2} + \cdots = 0$입니다.

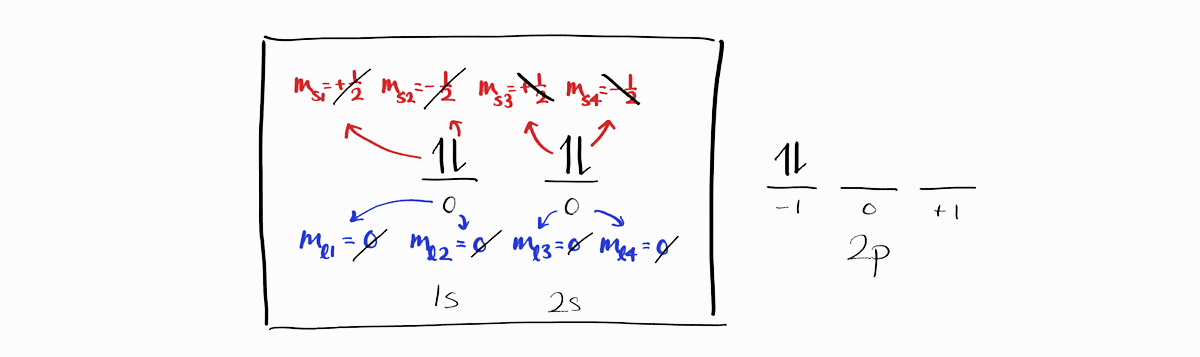
이러한 특성은 완전히 채워진 부껍질 모두에 해당하며, 아래는 $3d$ 부껍질의 예시입니다.

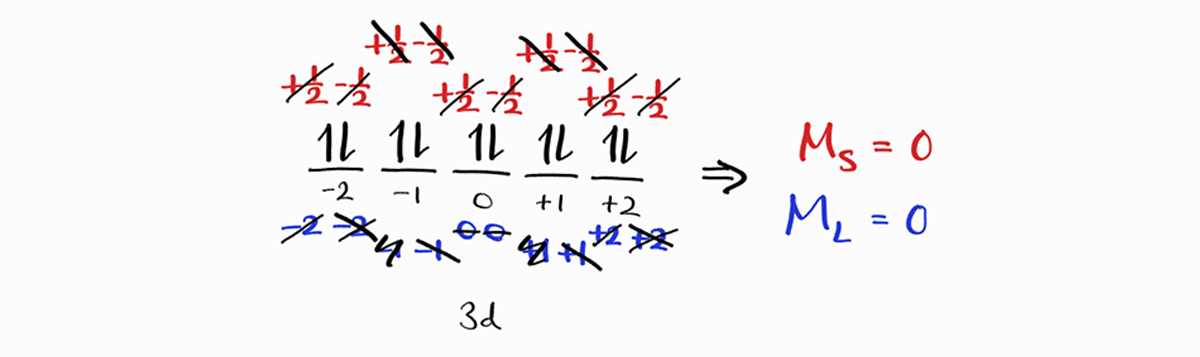
따라서,

완전히 채워진 부껍질은 총 $M_L$과 $M_S$에 기여하지 않습니다. 따라서 term symbol을 구할 때 무시할 수 있습니다.

$2p$ 부껍질에 있는 나머지 2개의 전자는 파울리 배타 원리에 부합하도록 6개의 spin orbital(스핀 궤도) 중 아무거나에 들어갈 수 있습니다.

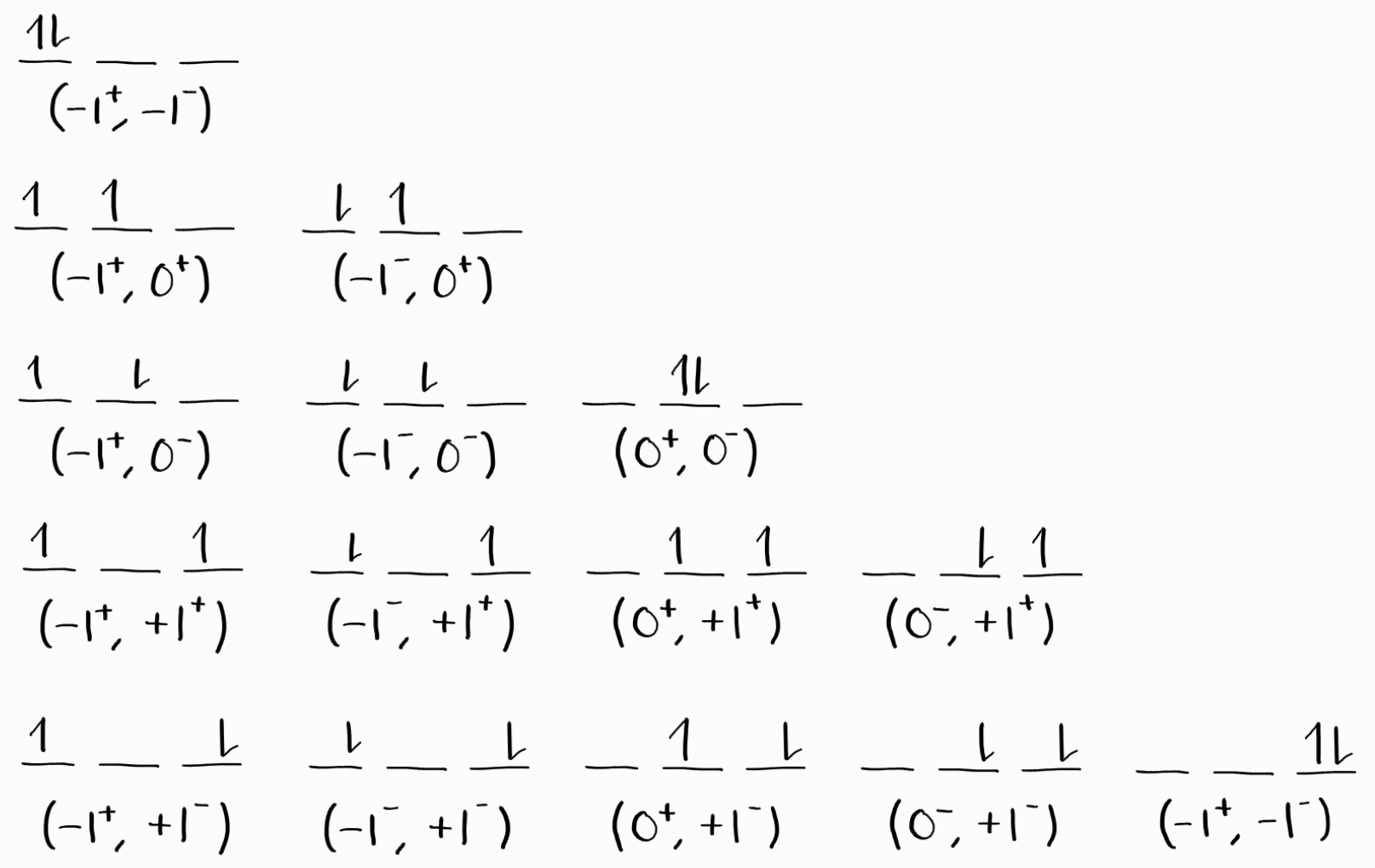
총 15개의 microstate가 있습니다. 수학적으로는 2개의 동등한 전자(equivalent electron)를 6개의 스핀 오비탈에 넣는 것은 6개의 스핀 오비탈 중 2개를 선택(중복하지 않고, 순서 상관없이)하는 것과 같습니다. 이를 일반화하여 $N$개의 동등한 전자를 $G$개의 스핀 오비탈에 배치하는 것의 microstate의 개수는 다음과 같습니다.

\[\frac{G!}{N!(G-N)!}\]

파트 2에서 보셨듯이 microstate의 개수는 실제 에너지 상태의 개수와 같습니다. 이런 microstate를 파트 2의 접근 방법 2처럼 $M_L$와 $M_S$에 따라 표로 분류합니다. 각 term symbol에 대하여 해당하는 $M_L$과 $M_S$인 microstate를 각각 하나씩 지웁니다. 이 과정을 반복하여 microstate가 더 이상 남아있지 않을 때까지(즉, 에너지 상태가 더 이상 남아있지 않을 때까지) term symbol을 찾으면 됩니다.

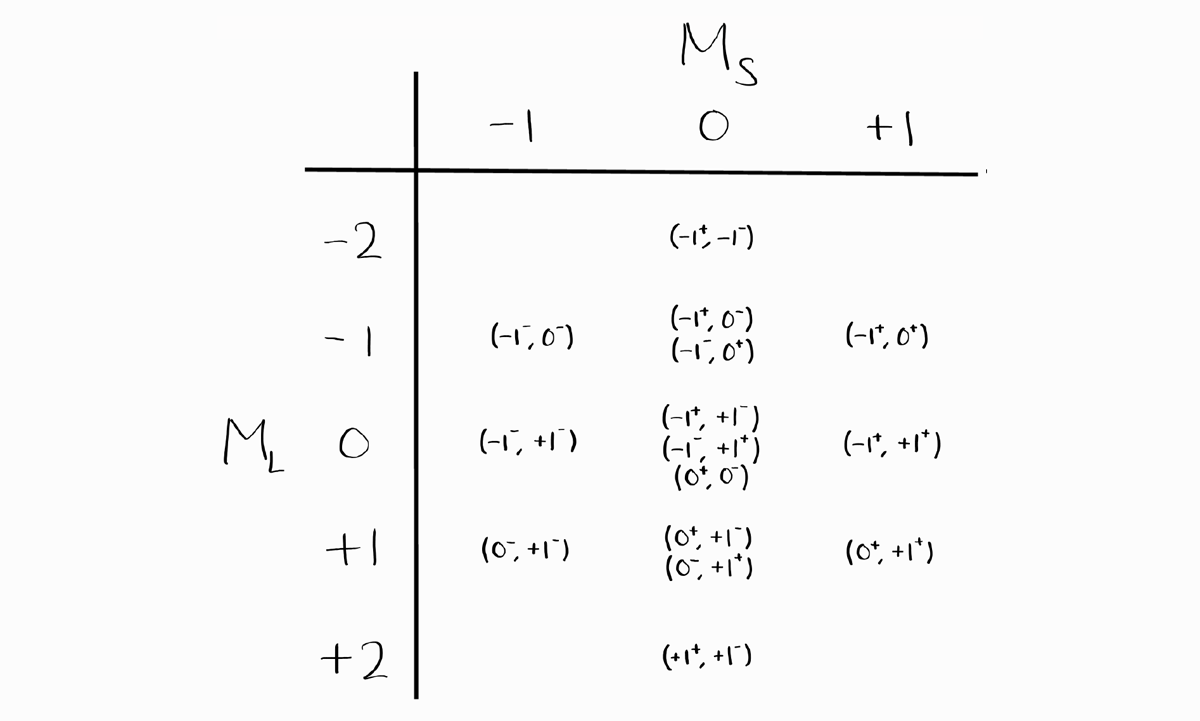
Term symbol을 추출하기 전에 이 표 자체에 대해 주목해봅시다. 이 표는 가로 및 세로로 대칭임을 알 수 있습니다. $M_L$과 $M_S$인 항목과 $-M_L$과 $M_S$인 항목, $M_L$과 $-M_S$인 항목, 마지막으로 $-M_L$과 $-M_S$인 항목은 단순히 각 전자의 $m_l$과 $m_s$의 부호가 다를 뿐입니다.

그리하여

Microstate 표를 만들 때:

1. 표의 1/4 정도를 먼저 채웁니다 (ex. $M_L \leq 0$ and $M_S \leq 0$)
2. 나머지 3/4은 가로와 세로 대칭성을 토대로 완성합니다.
3. Microstate의 갯수가 맞는지 해야려 점검합니다.

참고로 전자 배치를 먼저 그린 후 microstate 표를 만들지 말고 microstate 표를 만들면서 시작하면 시간을 많이 절약할 수 있습니다.

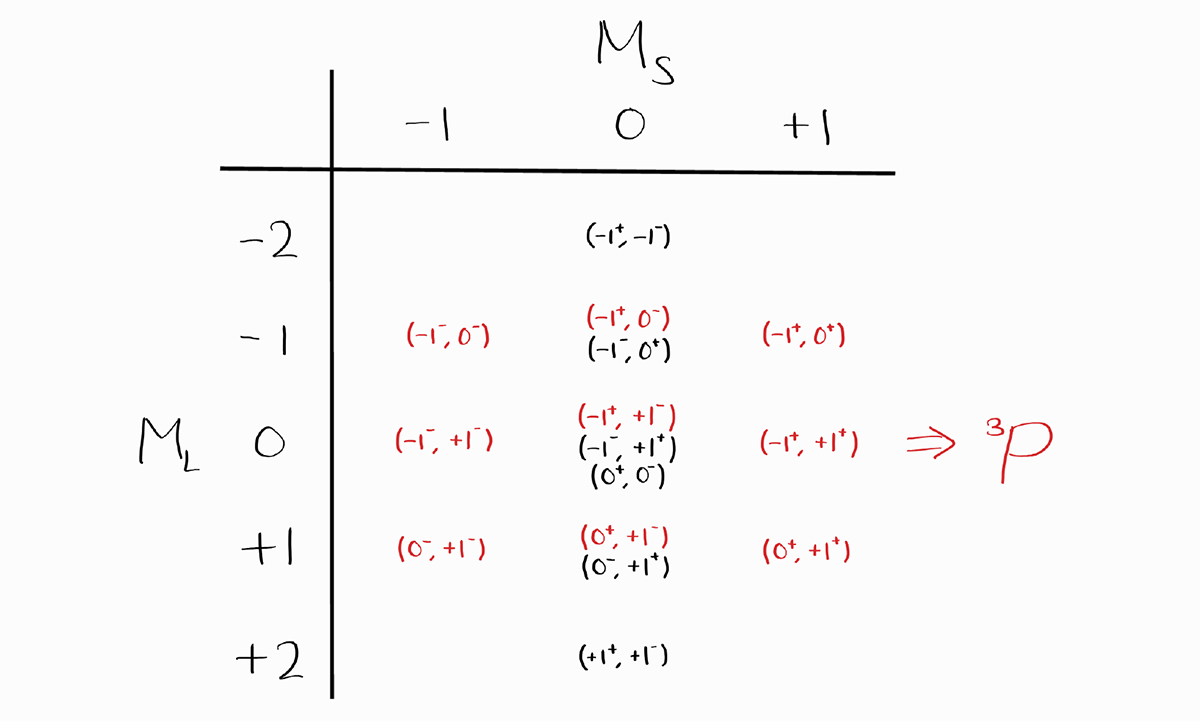
이 표에서 $M_S$의 최댓값이 +1이라서 $S = 1$이며 동시에 가능한 $M_L$의 최댓값이 +1이라서 $L = 1$이므로 첫 번째 term symbol은 $^3P$입니다. 이후 $^3P$에 해당하는 $M_L$과 $M_S$에 해당하는 항목 한 개씩을 지웁니다.

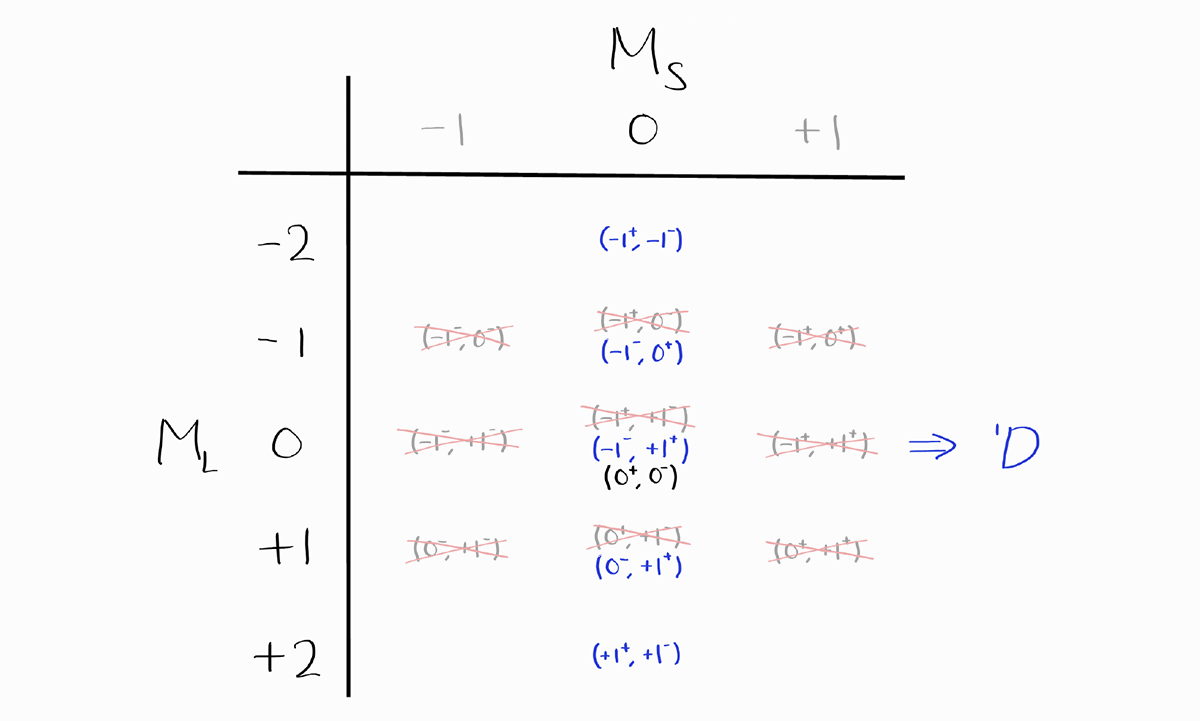
이번에 $M_S = 0$이라서 $S = 0$이며 $M_L$의 최댓값이 +2이라서 $L = 2$이므로 두 번째 term symbol은 $^1D$입니다.

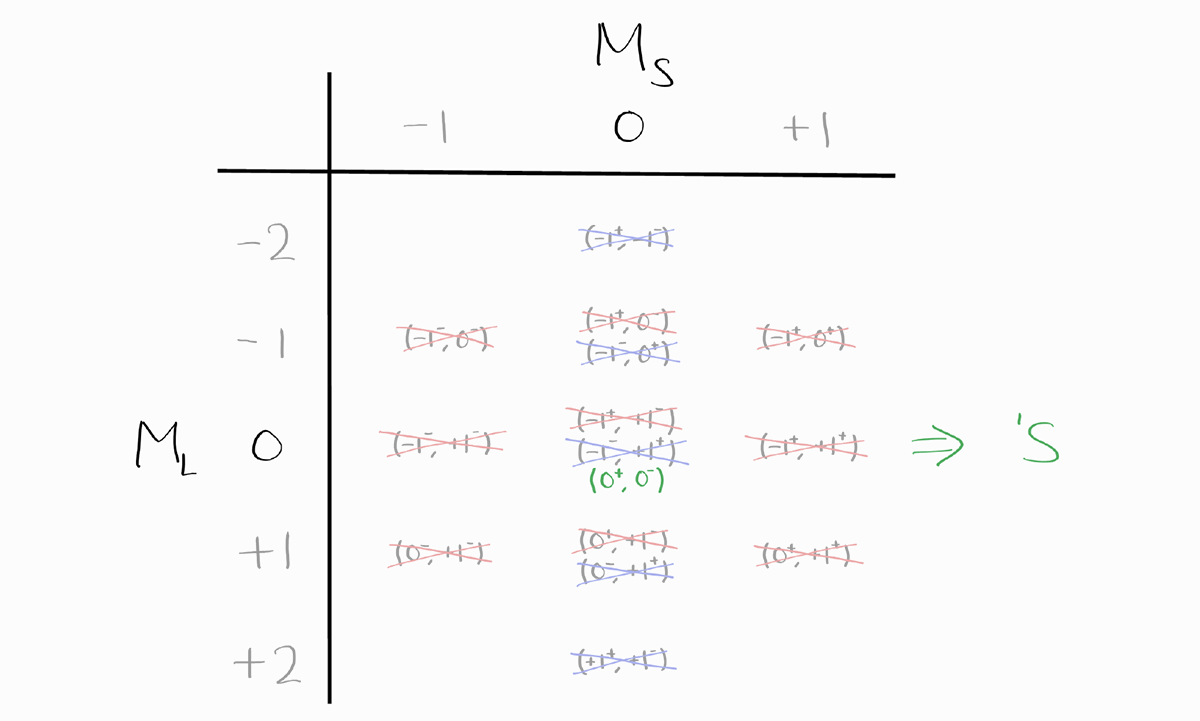
마지막으로 $M_S = 0$이고 $M_L = 0$이라서 $S = 0$, $L = 0$이므로 남은 term symbol은 $^1S$입니다.

Term symbol은 이렇게 구하였습니다:

아직 $J$의 값이 결정되지 않았으므로 term symbol을 확정 짓지 못하였습니다. 다시금 되돌아보면 $J$는 $\left|L - S\right|,\,\cdots,\,L + S$의 값을 가집니다.

$^3P$ ($L = 1$, $S = 1$)의 경우 $J_{\text{min}} = 0$이고 $J_{\text{max}} = 2$입니다. 따라서 $J = 2,\, 1,\, 0$이고 term symbol은 $^3P_2$, $^3P_1$, $^3P_0$입니다.

$^1D$ ($L = 2$, $S = 0$)의 경우 $J_{\text{min}} = 2$이고 $J_{\text{max}} = 2$입니다. 따라서 $J = 2$이고 term symbol은 $^1D_2$입니다.

$^1S$ ($L = 0$, $S = 0$)의 경우 $J_{\text{min}} = 0$이고 $J_{\text{max}} = 0$입니다. 따라서 $J = 0$이고 term symbol은 $^1S_0$입니다.

그리하여 $1s^22s^22p^2$의 term symbol은, 혹은 모든 $np^2$ 전자배치의 term symbol은 다음과 같습니다.

가능한 Term symbol의 표

위 과정을 통해 다양한 전자 배치에 대하여 term symbol을 정리할 수 있습니다.

전자 배치	Term symbol ($J$ 제외)
$s^1$	$^2S$
$p^1$; $p^5$	$^2P$
$p^2$; $p^4$	$^3P$, $^1D$, $^1S$
$p^3$	$^4S$, $^2D$, $^2P$
$d^1$; $d^9$	$^2D$
$d^2$; $d^8$	$^3F$, $^3P$, $^1G$, $^1D$, $^1S$
$d^3$; $d^7$	$^4F$, $^4P$, $^2H$, $^2G$, $^2F$, $^2D(\text{two})$, $^2P$
$d^4$; $d^6$	$^5D$, $^3H$, $^3G$, $^3F(\text{two})$, $^3D$, $^3P(\text{two})$, $^1I$, $^1G(\text{two})$, $^1F$, $^1D(\text{two})$, $^1S(\text{two})$
$d^5$	$^6S$, $^4G$, $^4F$, $^4D$, $^4P$, $^2I$, $^2H$, $^2G(\text{two})$, $^2F(\text{two})$, $^2D(\text{three})$, $^2P$, $^2S$
$s^2$; $\,p^6$; $\,d^{10}$; $\,\cdots$	$^1S$

이 표에서 주목할 것은 총 세 가지가 있습니다.

먼저 같은 term symbol이 2개 이상 있는 전자 배치가 있는 것을 일부 볼 수 있습니다. 이는 앞서 다루지 않았던, 같은 전자 배치 및 $L$, $M_L$, $S$, $M_S$를 지닌 에너지 상태가 2개 이상 있는 예외입니다. 이런 경우 에너지 상태 또는 에너지 준위를 특정하는데 사용되는 에너지를 전자 배치만으로 대체할 수 없습니다.

두 번째는 완전히 채워진 부껍질로만 이루어진 전자 배치의 term symbol은 오직 $^1S$이라는 점입니다. 이는 모든 전자에 대하여 $m_l$과 $m_s$이 상쇄되어 $M_L = 0$, $M_S=0$이기 때문이며, $M_L$과 $M_S$ 뿐만 아니라 $M_J$도 무조건 0입니다. 이에 따라 $J = 0$이며 term symbol은 항상 $^1S_0$입니다.

무엇보다 중요한 마지막 포인트는 빈 전자 구멍인 양공과 관련된 팁입니다. 양공이 몇 개 있는 전자 배치와 같은 개수의 전자가 같은 부껍질에 있는 전자 배치는 같은 term symbol을 가집니다. 다른 말로는 빈 부껍질에 전자 $n$개를 넣는 것과 완전히 채워진 부껍질에서 전자 $n$개를 빼는 것이 각운동량의 관점에서는 같다는 것을 의미합니다. 즉, 양공은 전자와 비슷하게 전체 각운동량에 기여합니다.

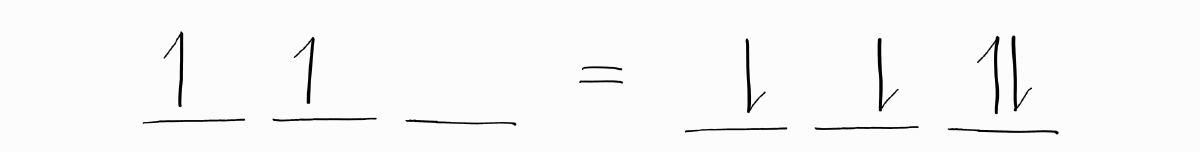
따라서 양공을 전자로 바꾸어 $L$과 $S$를 구해도 아무런 문제가 없으며 때로 이 방법이 더 쉬울 수 있습니다.

예시 2: 들뜬 $1s^22s^22p^43p^2$ 네온

여태까지 배웠던 점 중 세 가지를 $1s^22s^22p^43p^2$ 전자 배치를 가지는 들뜬 네온을 통해 복습해봅시다.

1. 완전히 채워진 부껍질은 전체 $M_L$과 $M_S$에 기여하지 않음으로 term symbol을 구할 때 무시할 수 있습니다.
2. 양공을 전자로, 전자를 양공으로 바꾸어 $L$과 $S$를 구해도 됩니다.
3. (파트 2에서) 양자수 $j_1$와 $j_2$로 표현되는 두 각운동량의 합은 전체 각운동량 양자수 $J$를 만들어내며 이는 $ J=\left|j_1 - j_2\right|,\,\cdots,\,j_1 + j_2$ 값을 가집니다.

1번에 따르면 $1s^22s^22p^43p^2$ 전자 배치에서 완전히 채워진 부껍질을 무시하고 $2p^43p^2$로만 term symbol을 구할 수 있습니다.

2번에 따르면 $2p^43p^2$ 전자 배치 대신 $2p$ 부껍질의 전자를 양공으로 바꾼 $2p^23p^2$ 전자 배치로 term symbol을 구할 수 있습니다.

남은 $2p^23p^2$ 전자 배치는 $2p^2$ 전자 배치와 $3p^2$ 전자 배치로 나눌 수 있습니다. 일반적인 (equivalent electron인) $np^2$의 term symbol($J$를 제외한)은 $^3P$, $^1P$, $^1S$입니다(이는 바닥 상태 탄소의 term symbol을 구할 때 나온 결과입니다). $2p^2$와 $3p^2$ 부껍질 사이(즉, non-equivalent electrons 사이)는 각각의 term symbol의 $L$과 $S$ (아래에는 $l_i$과 $s_i$로 표기함)를 3번에 따라 서로 “더하여” 새로운 $2p^23p^2$ 전자 배치의 term symbol을 구하고자 합니다.

A. $^3P$와 $^3P$의 합

Term Symbol	$l_i$	$s_i$
$^3P$	1	1
$^3P$	1	1

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
1	1	0	2	0, 1, 2

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
1	1	0	2	0, 1, 2

⇒ $^5D$, $^5P$, $^5S$, $^3D$, $^3P$, $^3S$, $^1D$, $^1P$, $^1S$

B. $^3P$와 $^1D$의 합

Term Symbol	$l_i$	$s_i$
$^3P$	1	1
$^1D$	2	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
1	2	1	3	1, 2, 3

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
1	0	1	1	1

⇒ $^3F$, $^3D$, and $^3P$

C. $^1D$와 $^3P$의 합

이는 B. $^3P$와 $^1D$의 합과 같음.

⇒ $^3F$, $^3D$, and $^3P$

D. $^3P$와 $^1S$의 합과 같음.

Term Symbol	$l_i$	$s_i$
$^3P$	1	1
$^1S$	0	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
1	0	1	1	1

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
1	0	1	1	1

⇒ $^3P$

E. $^1S$와 $^3P$의 합과 같음

이는 D. $^3P$와 $^1S$의 합과 같음.

⇒ $^3P$

F. $^1D$와 $^1D$의 합과 같음

Term Symbol	$l_i$	$s_i$
$^1D$	2	0
$^1D$	2	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
2	2	0	4	0, 1, 2, 3, 4

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
0	0	0	0	0

⇒ $^1G$, $^1F$, $^1D$, $^1P$, and $^1S$

G. $^1D$와 $^1S$의 합

Term Symbol	$l_i$	$s_i$
$^1D$	2	0
$^1S$	0	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
2	0	2	2	2

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
0	0	0	0	0

⇒ $^1D$

H. $^1S$와 $^1D$의 합

이는 G. $^1D$와 $^1S$의 합과 같음.

⇒ $^1D$

I. $^1S$와 $^1S$의 합

Term Symbol	$l_i$	$s_i$
$^1S$	0	0
$^1S$	0	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
0	0	0	0	0

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
0	0	0	0	0

⇒ $^1S$

결과적으로 $1s^22s^22p^43p^2$의 term symbol은 다음과 같습니다:

$^5D$, $^5P$, $^5S$, $^3F$ (two), $^3D$ (three), $^3P$ (five), $^3S$, $^1G$, $^1F$, $^1D$ (four), $^1P$ (two), and $^1S$ (three).

위 term symbol로부터 총 에너지 상태의 개수를 일일이 구한다면 225임을 알 수 있으며, 이 수는 $15\times 15$로 $1s^22s^22p^43p^2$의 microstate의 총 개수와 같음을 확인할 수 있습니다.

훈트 규칙과 바닥 상태

지금까지는 한 전자 배치의 모든 term symbol을 구하는 데 열중하였습니다. 이때 꼭 물어야 할 질문은 “이 term symbol 중 어떤 term symbol이 가장 안정한가요?”입니다. 다르게 표현하자면 “원자의 바닥 상태는 무엇일까요?”라고 할 수 있습니다.¹

원자의 바닥 상태 term symbol은 독일의 분광학자 프리드리히 훈트가 발견한 세 경험적 규칙으로 구할 수 있습니다.

1. $S$가 가장 큰 term symbol이 가장 안정합니다.
2. $S$가 같은 term symbol 중 $L$이 가장 큰 term symbol이 가장 안정합니다.

3. $S$와 $L$이 같은 term symbol의 경우 $J$를 통하여 바닥 상태 term symbol을 판단합니다.

   1. 반보다 더 적게 채워진 부껍질의 경우 $J$가 가장 작은 term symbol이 가장 안정합니다.
   2. 반보다 더 많이 채워진 부껍질의 경우 $J$가 가장 큰 term symbol이 가장 안정합니다.

예를 들어 바닥 상태 전자 배치인 $1s^22s^22p^2$ 탄소의 term symbol은 $^1S_0$, $^3P_2$, $^3P_1$, $^3P_0$, $^1D_2$입니다. 이중 $S$가 가장 큰 term symbol은 $^3P_2$, $^3P_1$, $^3P_0$입니다.

이 세 term symbol 모두 $L$이 같습니다.

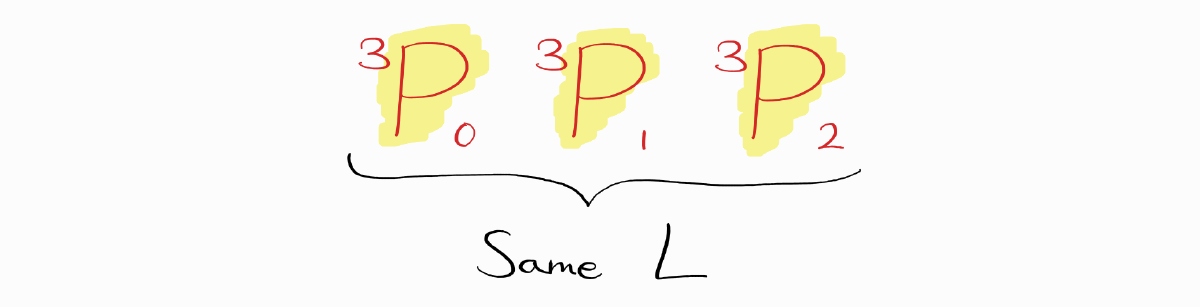
따라서 세 번째 규칙으로 넘어가 $J$로 바닥 상태 term symbol을 판단해야 합니다. $2p$ 부껍질이 반보다 더 적게 채워저있기 때문에 $J$가 가장 작은 term symbol을 골라야 합니다.

따라서 $^3P_0$가 탄소의 바닥 상태 term symbol입니다.

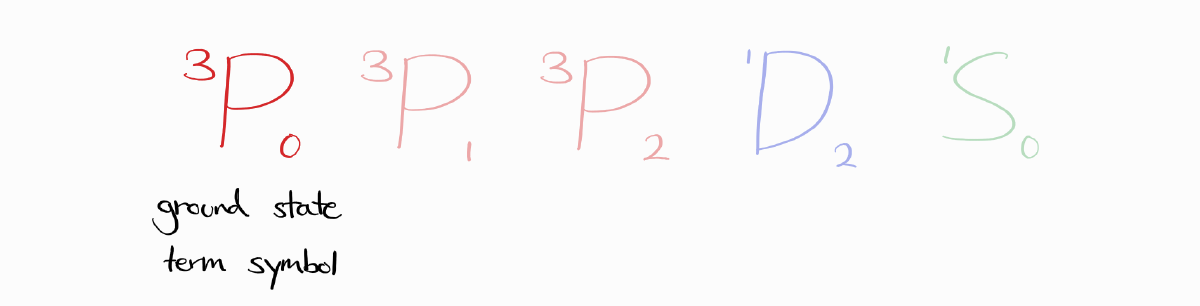
이를 파트 2에서 보았던 에너지 도표에 나타낼 수 있습니다.

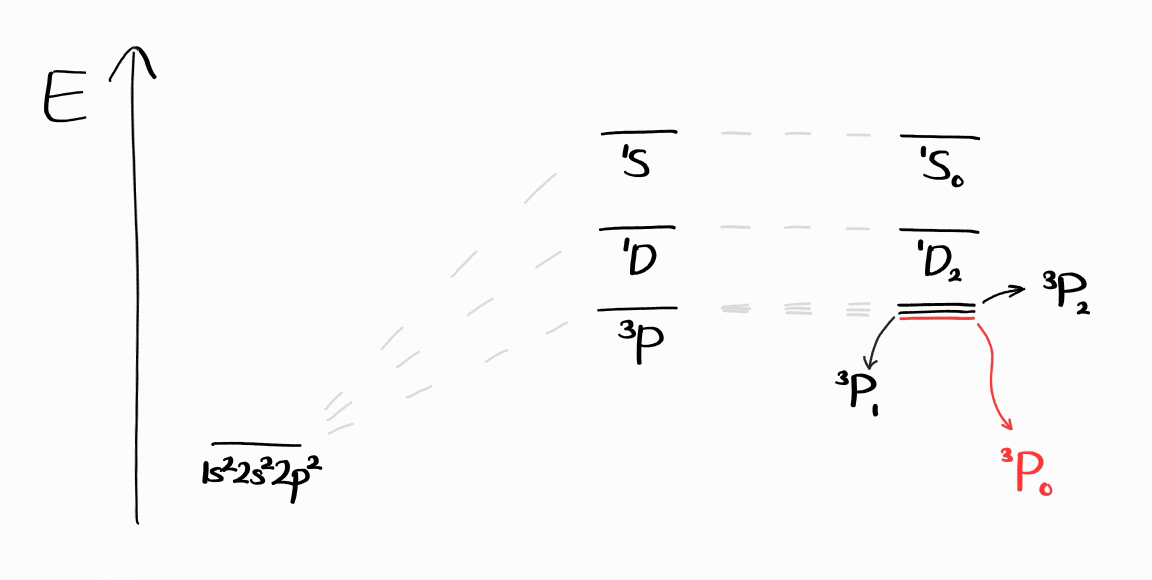
바닥 상태 term symbol을 알고 싶을 때 처음부터 모든 term symbol을 구할 필요가 없습니다. 바닥 상태 term symbol과 관련이 있는 microstate를 통해 바닥 상태 term symbol을 찾는 간단한 방법이 존재합니다. 우선 $M_S$가 가장 큰 microstate를 구해야 하며, 이는 일반화학의 휸트 규칙으로 “바닥 상태”를 구하는 것과 동일하고 양자역학적으로는 휸트 규칙에서 했던 것처럼 가장 큰 $S$를 가진 term symbol을 구하는 것과 동등합니다.

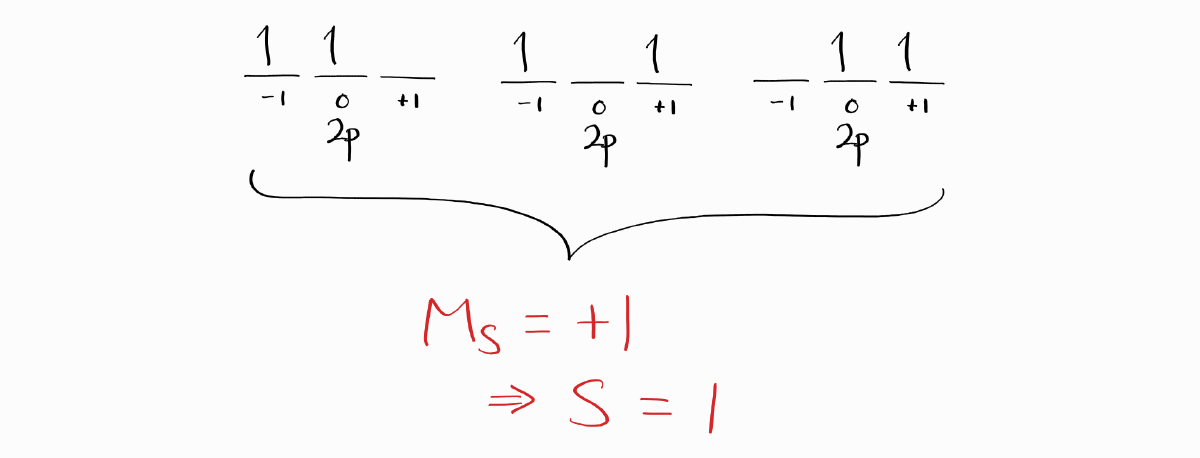
이 microstate 중 $L$을 최대화하기 위해 $M_L$이 가장 큰 microstate를 선택합니다.

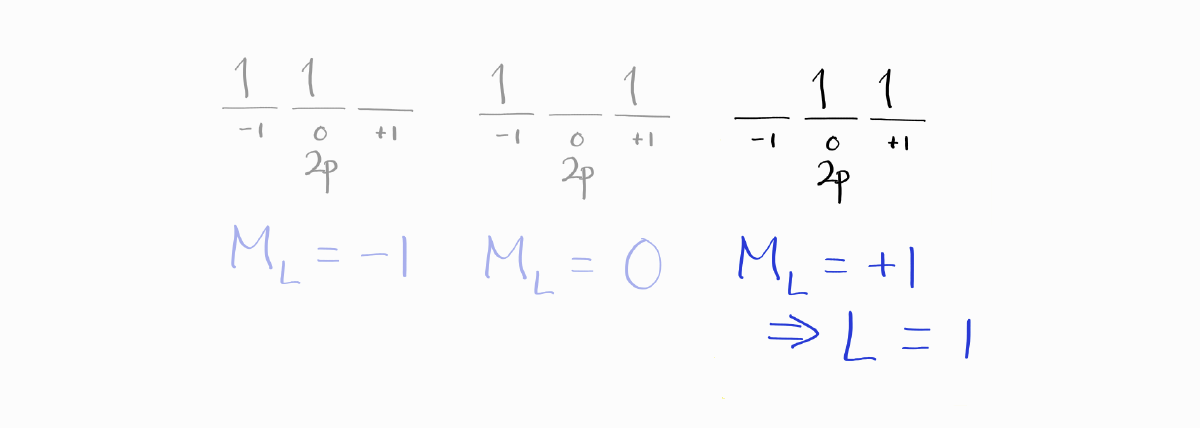
$S = 1$이고 $L = 1$이므로 $J$를 생략한 term symbol은 $^3P$입니다. $J$를 계산하고 적합한 $J$를 훈트 규칙에 의하여 선택하면 같은 바닥 상태 term symbol인 $^3P_0$에 도달하게 됩니다.

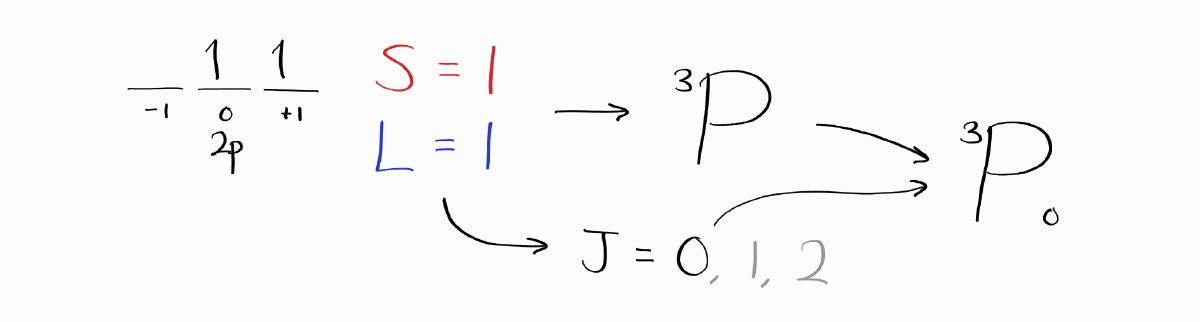
더 복잡한 예시는 바닥 상태 전자 배치가 $\left[\text{Ar}\right]3d^54s^2$인 망가니즈입니다. Microstate의 총 개수는 252이며 term symbol은 총 16개가 있습니다. 따라서 모든 term symbol을 구한 후 바닥 상태 term symbol을 구하는 것은 무척이나 어려울 뿐만 아니라 틀리기도 쉽습니다. 하지만, 위의 방법을 활용하면 망가니즈의 바닥 상태 term symbol을 매우 쉽게 구할 수 있습니다.

우선 $M_S$이 가장 큰 microstate를 구합니다.

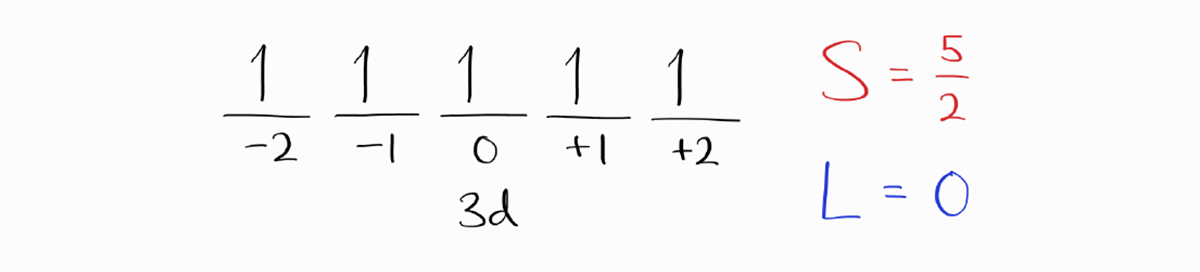
공교롭게도 하나의 microstate만 남았으며, $M_L = 0$입니다. 따라서 $L=0$이며 $J$를 생략한 term symbol은 $^6S$입니다.

이제 $J$로 바닥 상태 term symbol을 구해야 합니다. 하지만 $3d$ 부껍질이 정확히 반만 채워져 있는 것이 난감할 수 있습니다. 다행히도 이 경우 가능한 $J$는 오직 $5/2$이므로 바닥 상태 term symbol은 $^6S_{5/2}$입니다.

훈트 규칙은 바닥 상태 전자 배치에 거의 완벽하게 적용되지만 다른 들뜬 상태 전자 배치의 경우 부정확한 결과가 나올 수 있습니다. 또한 훈트 규칙은 term symbol 사이의 에너지 순서를 판단하기에는 부적절합니다. 간단히 말하자면 훈트 규칙은 바닥 상태를 구할 때만 사용하는 것이 적합합니다.

결론

한 전자 배치의 모든 term symbol을 구할 때:

1. 완전히 채워진 부껍질은 무시합니다.
2. 각 부껍질마다 부껍질이 반보다 더 많이 채워진 경우 양공을 전자로 바꾸어 생각합니다.
3. 각 부껍질의 동등한 전자(equivalent electron)에 대하여 $l_i$와 $s_i$를 구합니다. 이때 microstate 표를 만들어서 구하거나 서적 등 자료를 참고합니다.
4. 모든 부껍질의 $l_i$과 $s_i$를 더하여 (즉, 이번에는 non-equivalent electrons끼리 더함) 전체 $L$과 $S$를 구합니다.
5. 각 $L$과 $S$의 조합마다 $J$를 구합니다.

모든 term symbol을 이미 알 때 바닥 상태 term symbol을 구하는 방법 - 훈트 규칙:

1. $S$가 가장 큰 term symbol이 가장 안정합니다.
2. $S$가 같은 term symbol 중 $L$이 가장 큰 term symbol이 가장 안정합니다.

3. $S$와 $L$이 같은 term symbol의 경우 $J$를 통하여 바닥 상태 term symbol을 판단합니다.

   1. 반보다 더 적게 채워진 부껍질의 경우 $J$가 가장 작은 term symbol이 가장 안정합니다.
   2. 반보다 더 많이 채워진 부껍질의 경우 $J$가 가장 큰 term symbol이 가장 안정합니다.

Term symbol을 모르는 상태에서 바닥 상태 term symbol을 구하는 방법:

1. $M_S$가 가장 큰 microstate부터 시작하며 이 $M_S = S$입니다.
2. $M_L$가 가장 큰 microstate를 선택하며 이 $M_L = L$입니다.
3. $L$과 $S$로 $J$를 계산합니다. 훈트 규칙으로 알맞은 $J$의 값을 구합니다.

각주

1. 대부분의 서적이 가장 안정한 term symbol을 “바닥 상태”라고 부르지만, 이는 더 엄밀하게 “바닥 에너지 준위”입니다. 이 글은 시중의 서적에 맞춰 바닥 에너지 준위 term symbol을 “바닥 상태 term symbol”이라고 부릅니다. ↩