The pKa of Water ... and more

Disclaimer

This article argues that the $\text{p}K_{\text{a}}$ of water is $14.0$, not $15.7$ as stated by most organic chemistry textbooks. Unless you can convince your organic chemistry teacher/professor, stick to $15.7$.

This article is based off of three sources.

On the $\text{p}K_{\text{a}}$ of water:

• What is the pKa of water? on LibreTexts
• pKa Values in the Undergraduate Curriculum: What Is the Real pKa of Water? by Silverstein and Heller, published in the Journal of Chemical Education

And on $\text{p}K_{\text{a}}$ in general:

• pKa Values in the Undergraduate Curriculum: Introducing pKa Values Measured in DMSO to Illustrate Solvent Effects by Silverstein and Heller

14.0 or 15.7

The $\text{p}K_{\text{a}}$ of water, according to any general chemistry textbook, is $14.0$ ¹. However, in most organic chemistry textbooks and resources, the $\text{p}K_{\text{a}}$ of water is $15.7$.

Here is one example in the textbook Organic Chemistry by David Klein.

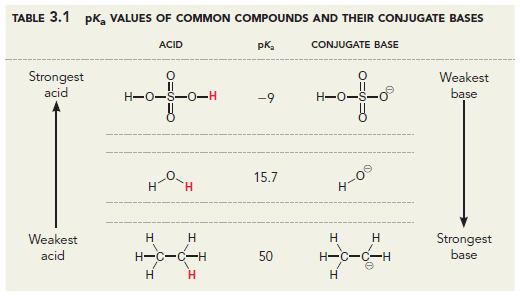
Here is another from the widely used $\text{p}K_{\text{a}}$ table by Ripin and Evans.

The rationale for this value is as follows². Below is the equation for the acid dissociation constant $K_\text{a}$, in terms of activities of each chemical species³.

$$K_\text{a} = \frac{a_{\text{H}^{+}} a_{\text{OH}^{-}}}{a_{\text{H}_2\text{O}}}$$

For dilute solutions, activity is well approximated by molarity⁴. Thus, $a_{\text{H}^{+}} = \left [ \text{H}^{+} \right ]$ and $a_{\text{OH}^{-}} = \left [ \text{OH}^{-} \right ]$. In addition, we know for pure water that $\left [ \text{H}^{+} \right ] = 1.0 \times 10^{-7} \, \text{M}$ and $\left [ \text{OH}^{-} \right ] = 1.0 \times 10^{-7} \, \text{M}$.

The only value left to determine is $a_{\text{H}_2\text{O}}$. Instead of treating water as a solvent and taking this value as unity (as $1$), we treat water as a solute and use the molarity of pure water for the activity of water.

Let us now calculate the molarity of pure water. The molar mass of water is $18.015 \, \text{g/mol}$, and its density at $25 ^{\circ} \text{C}$ is $997 \, \text{g/L}$. Therefore, the molar concentration of water $\left [ \text{H}_{2}\text{O} \right ]$ is $55.3 \, \text{M}$. We plug this value in to obtain $\text{p} K _{\text{a}} = 15.7$.

The calculation above is wrong for three reasons.

1. The activity of water should be taken as unity and only unity: pure substances in their reference state have their activities as set to $1$.
2. The term ‘concentration’ for the molar concentration of water implies that water can be viewed as both a solvent and a solute, which is not possible.
3. Even if this was possible, $\left [ \text{H}_{2}\text{O} \right ] = 55.3 \text{M}$ is too large to be considered as dilute. Thus, one cannot approximate the activity of water with its molar concentration.

This may seem like a silly mistake; one may ask why such error is very widespread. This is well laid out in the aforementioned “What is the pKa of water?” article. In essence, this mistake was first made by prominent chemists like Brønsted who were just as confused as you. After a while, some other physical organic chemists also made the same mistake while trying to indirectly obtain the $\text{p}K_{\text{a}}$ of water. Then it made its way to countless publications, textbooks, and $\text{p}K_{\text{a}}$ tables without being scrutinized, and now thousands and millions of chemistry students are left to suffer from the resulting confusion.

The correct way of obtaining the $\text{p}K_{\text{a}}$ of water continues from $\left [ \text{H}^{+} \right ] = 1.0 \times 10^{-7} \text{M}$ and $\left [ \text{OH}^{-} \right ] = 1.0 \times 10^{-7} \text{M}$.

$$K_\text{a} = \frac{1.0 \times 10^{-14}}{a_{\text{H}_{2}\text{O}}} = 1.0 \times 10^{-14}$$

The activity of water is taken as unity (as $1$), and even though this ‘$1$’ is mathematically insignificant, it is very important in chemistry. It signifies that water is in its reference state as a pure liquid. Thus, the resulting $\text{p}K_{\text{a}} = 14.0$ automatically implies that water is the solvent and not a solute. This emphasis on the solvent will prove to be very important for the rest of the article.

Water as Both Solvent and Acid

Although we have established that the $\text{p}K_{\text{a}}$ of water is indeed $14.0$, we must take care when using this result. Below is an easy example.

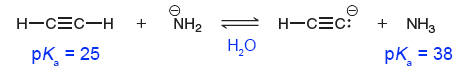
Because acetylene has a smaller $\text{p}K_{\text{a}}$ than ammonia, it is the stronger acid.

More specifically, acetylene is a stronger acid in ammonia in water, as the $\text{p}K_{\text{a}}$ values assume the solvent to be water.

Here’s another example.

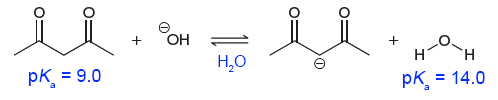
In this case, acetylacetone (the 1,3-diketone on the far left) is a stronger acid than water as both solvent and acid. If we wanted to compare the acid strength of acetylacetone and water both as an acid/solute, we must use a solvent other than water.

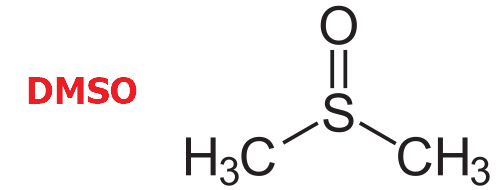
When dissolved in dimethyl sulfoxide (DMSO), acetylacetone and water now have a new $\text{p}K_{\text{a}}$. In practice, this still is referred to as $\text{p}K_{\text{a}}$. However, to reduce confusion, we will denote this new $\text{p}K_{\text{a}}$ as $\text{p}K_{\text{a}}^{\ast}$.

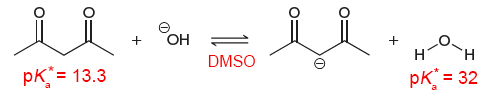
From the $\text{p} K_{\text{a}}^{\ast}$ of acetylacetone and water, we can conclude that acetylacetone is a stronger acid than water as acid/solute (in DMSO).

One Caveat

One caveat of the method above, using different solvents, is the fact for some rare cases, the strength of some acids may differ from solvent to solvent.

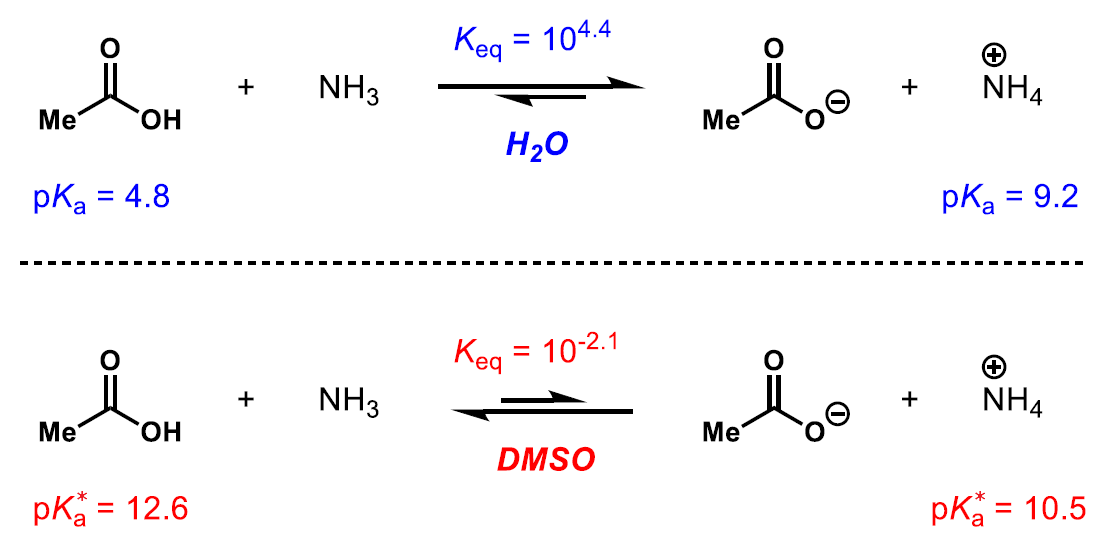
For example, in water, acetic acid is a stronger acid than the ammonium ion (top equilibrium). However, in DMSO, the acid strength is reversed and the ammonium ion is a stronger acid than acetic acid (bottom equilibrium).

pKa ≠ Acid Strength?

When learning organic chemistry, there is this notion that the strength of an acid is inherent. The $\text{p}K_{\text{a}}$ is thought of as a measure of such inherent property. The fact is, as we have seen above, the strength of an acid is not inherent and rather depends on a variety of factors, namely the solvent. It is a mistake to use the $\text{p}K_{\text{a}}$ (based on water) for a solvent vastly different from water, such as DMSO.

That being said, the $\text{p}K_{\text{a}}$ is not too terrible for judging the strength of an acid in any solvent, water or not. Below is a graph of $\text{p}K_{\text{a}}$ and $\text{p}K_{\text{a}}^{\ast}$. In general, as $\text{p}K_{\text{a}}$ increases, $\text{p}K_{\text{a}}^{\ast}$ increases linearly. In essence, strong acids are strong acids and weak acids are weak acids, irrespective of the solvent.

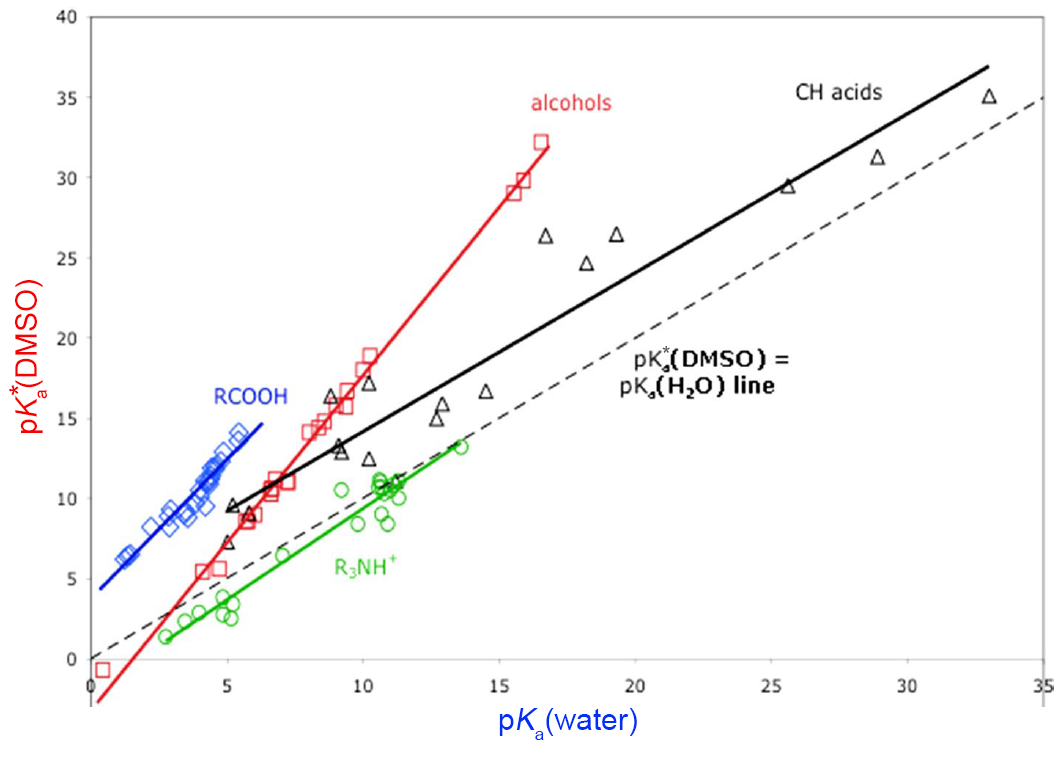
Simply put:

For acid-base equilibria in polar protic solvents (like methanol and acetic acid), the $\text{p}K_{\text{a}}$ is a very good predictor of acid strength, as how various chemical species are dissolved is similar to water.

For acid-base equilibria in polar aprotic solvents (like acetone or THF), the $\text{p}K_{\text{a}}$ is an acceptable predictor of acid strength. $\text{p}K_{\text{a}}^{\ast}$ (with DMSO as solvent), on the other hand, is a much better predictor of acid strength. When possible, use $\text{p}K_{\text{a}}^{\ast}$ not $\text{p}K_{\text{a}}$ for polar aprotic solvents.

Conclusion

1. The $\text{p}K_{\text{a}}$ of water (with water as its solvent) is without doubt $14.0$, not $15.7$
2. The acid strength of ‘water as both solvent and acid’ differs from the acid strength of ‘water only as acid’.
3. Acid strength is not an inherent property: the solvent in which acid-base equilibria occurs appreciably affects the strength of an acid.

Addendum

There is an entire book devoted to acid-base equilibria in various solvents. Check this out for more in-depth information.

• Acids and Bases: Solvent Effects on Acid-Base Strength by Brian G. Cox

Footnotes

1. $25 ^{\circ} \text{C}$, $1 \, \text{atm}$ or $1 \, \text{bar}$, depending on the source. ↩

2. Actually, this is just one of many ways of obtaining $\text{p}K_{\text{a}} = 15.7$. For a more complete explanation, including the most complete derivation of $\text{p}K_{\text{a}} = 14.0$ using the Gibbs free energy, see “What is the pKa of water?”. ↩

3. Activity is the “effective concentration” of chemical species. To learn more, check out this article. ↩

4. The proper way to relate activity and molar concentration is by using the equation $a = \gamma \frac{c}{c^{\circ}}$, where $\gamma$ is the activity coefficient (dependent on solvent, solute, concentration, etc.) which approaches unity (the value $1$) as the concentration approaches $0 \, \text{M}$ (infinite dilution). $c$ is the molarity and $c^{\circ}$ is the standard concentration, usually set as $1 \, \text{M}$. Note how the activity $a$ is a dimensionless quantity - this is the conclusive reason why all equilibrium constants are dimensionless. ↩