Atomic Term Symbols: Part 3 - Hund's Rule and More

Introduction

This article is an in-depth explanation on atomic term symbols based on Quantum Chemistry by Levine to supplement chapter 8 of Physical Chemistry: A Molecular Approach by McQuarrie. A good understanding of preceding chapters, notably chapters 6 and 7, is required.

The notation used in this article is based on the latter textbook.

In the preceding Part 1 and 2, we went over the theoretical background of multi-electron atoms and term symbols. In this article, we are going to go over tips and tricks regarding term symbols, as well as Hund’s rule.

Example: Carbon $1s^22s^22p^2$

$1s^22s^22p^2$ carbon consists of 6 electrons, which is a lot compared to our previous examples. The following are some of the microstates of $1s^22s^22p^2$.

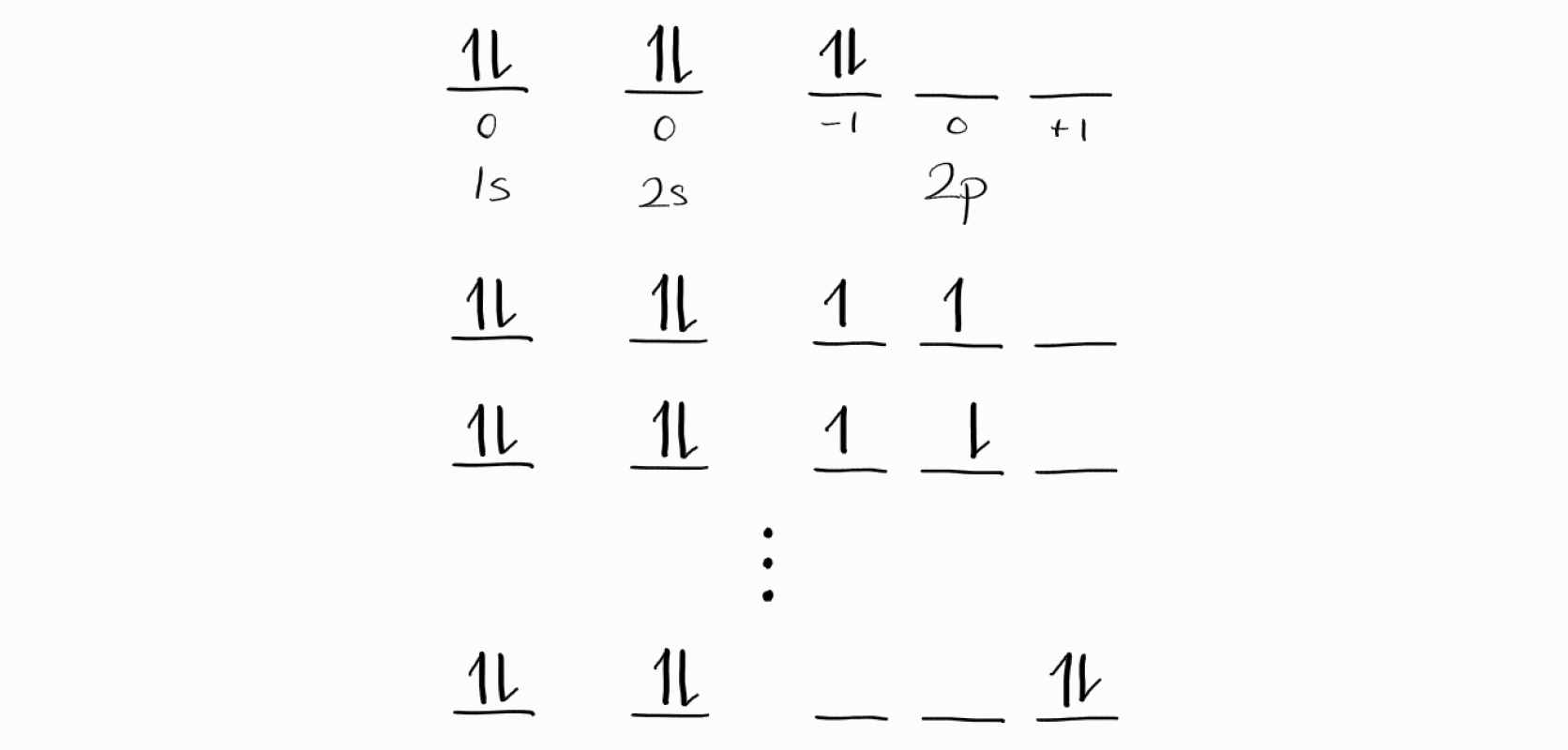
For all microstates, the four electrons of $1s$ and $2s$ subshells are the same. In addition, for these four electrons, the $M_L = m_{l1} + m_{l2} + \cdots = 0$ and $M_S = m_{s1} + m_{s2} + \cdots = 0$ as they cancel each other out.

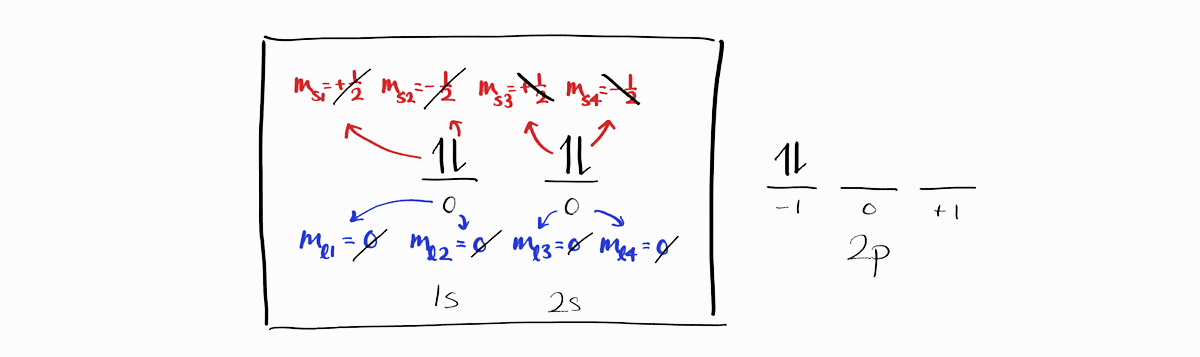
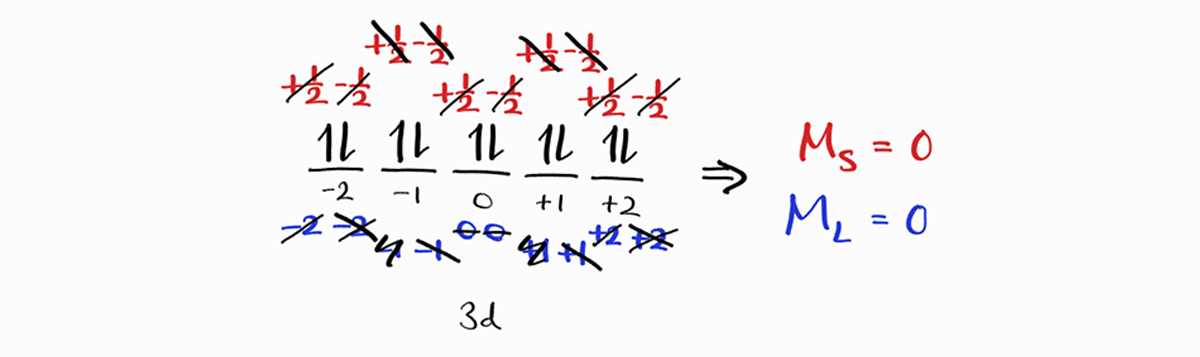
This is true for any filled subshells, like the $3d$ subshell below.

Therefore,

Completely filled subshells do not contribute to the overall $M_L$ and $M_S$. Therefore, they can be ignored when determining term symbols.

As for the remaining two electrons of the $2p$ subshell, they can occupy any of the six spin orbitals in a way that obeys the Pauli exclusion principle, as shown below.

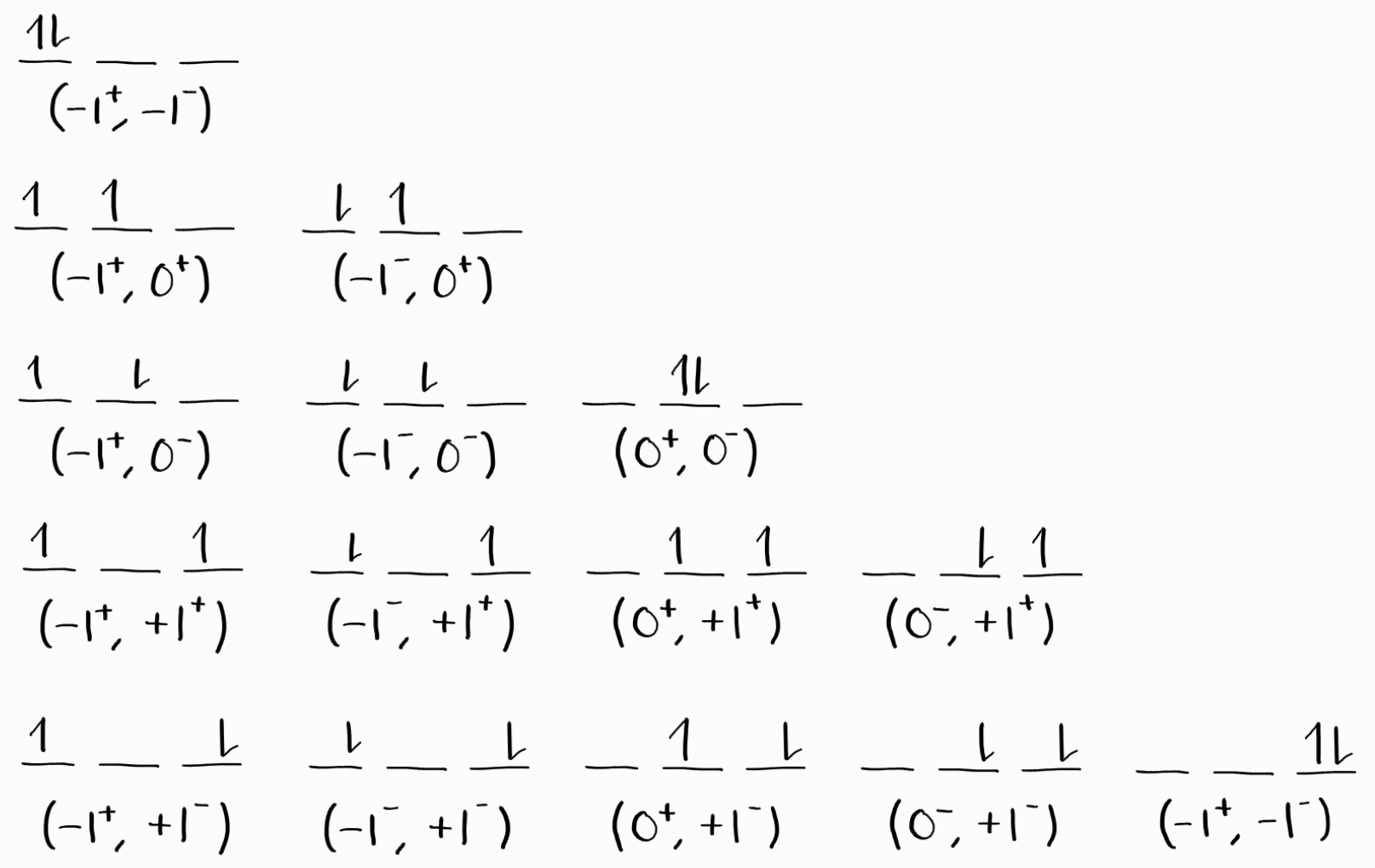
This results in 15 microstates. Mathematically speaking, assigning 2 equivalent electrons to 6 spin orbitals is the same as choosing 2 spin orbitals (without repetition nor order) out of a total of 6. In general, $N$ equivalent electrons and $G$ spin orbitals results in the following number of microstates.

\[\frac{G!}{N!(G-N)!}\]

The number of microstates is equal to the number of actual states, as shown in part 2. Similar to approach 2 of part 2, we organize these microstates into a table, according to their $M_L$ and $M_S$. For each term symbol, we cancel one microstate from each of the the possible $M_L$ and $M_S$ for that term symbol. We finish when there are no microstates remaining (thus no states remaining as well).

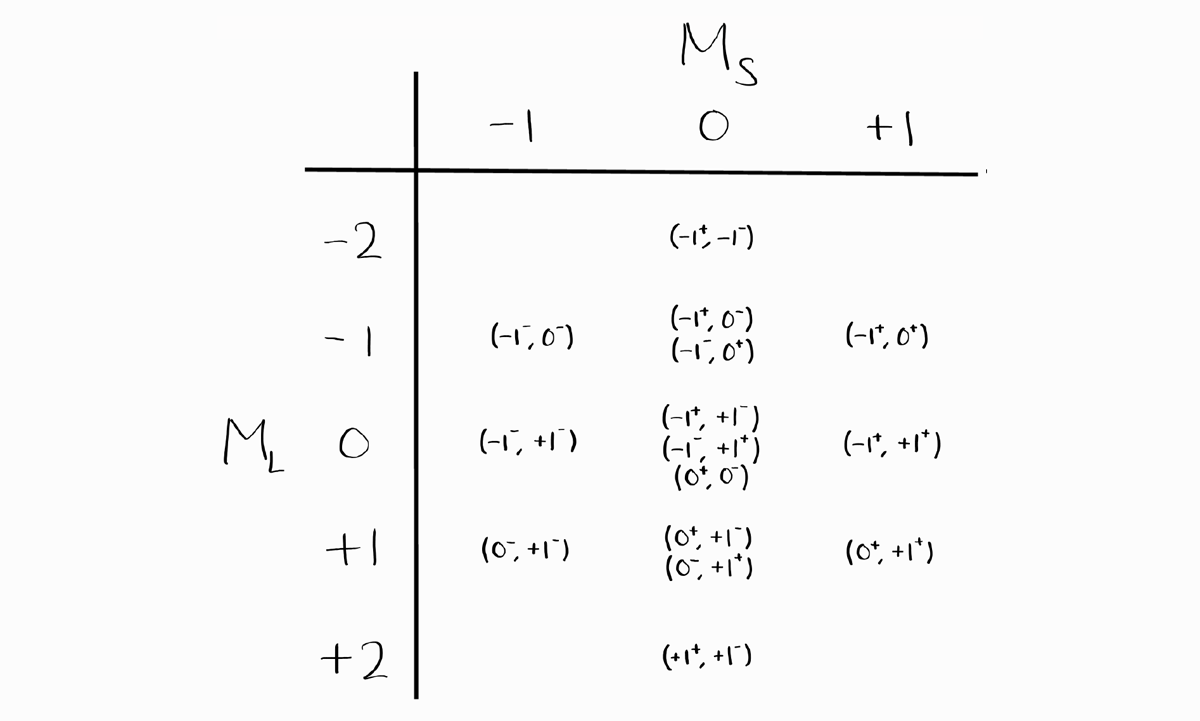
Before we deal with term symbols, notice how this table is symmetric vertically and horizontally. The entries of $M_L$ and $M_S$, of $-M_L$ and $M_S$, of $M_L$ and $-M_S$, and finally of $-M_L$ and $-M_S$ only differ in the sign of $m_l$ and $m_s$ of each electron.

Therefore,

When setting up a table of microstates:

1. Fill in the entries for one quadrant (ex. $M_L \leq 0$ and $M_S \leq 0$)
2. Fill the remaining quadrants by exploiting the vertical and horizontal symmetry of the table.
3. Finish by counting all the entries and checking if the total number of microstates is correct.

Note that the process of drawing electron configurations and then filling in the table of microstates is somewhat redundant; save time by just starting with the table of microstates.

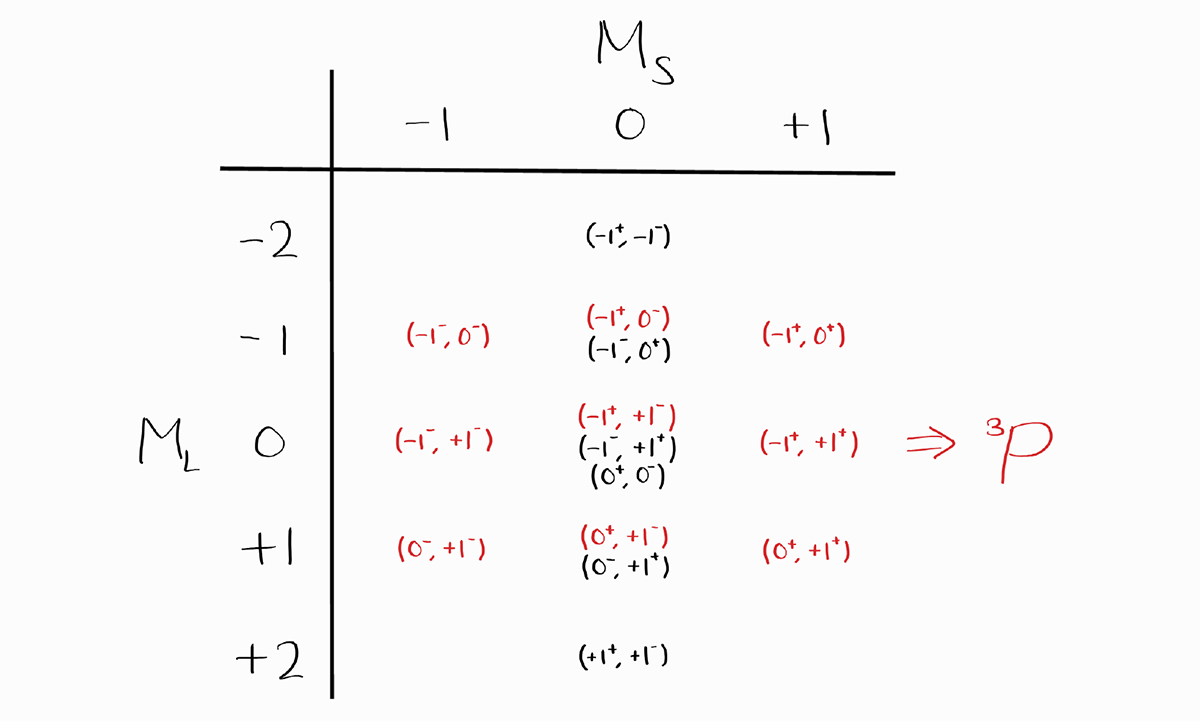
The first term symbol that arises from this table is $^3P$, as the largest value of $M_S = +1$ (which implies $S = 1$) and simultaneously, the largest possible value of $M_L = +1$ (which implies $L = 1$). We cross out one entry from each $M_L$ and $M_S$ possible for $^3P$.

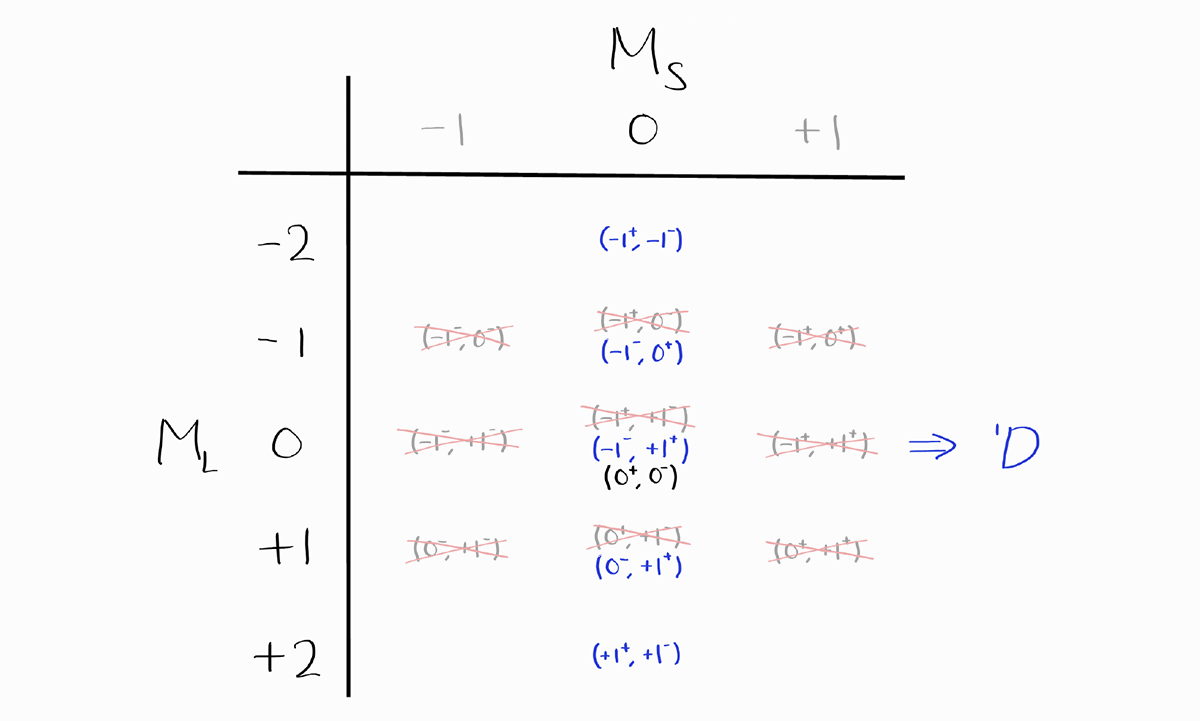
The next term symbol is $^1D$, as $M_S = 0$ (which implies $S = 0$) and the largest value of $M_L = +2$ (which implies $L = 2$).

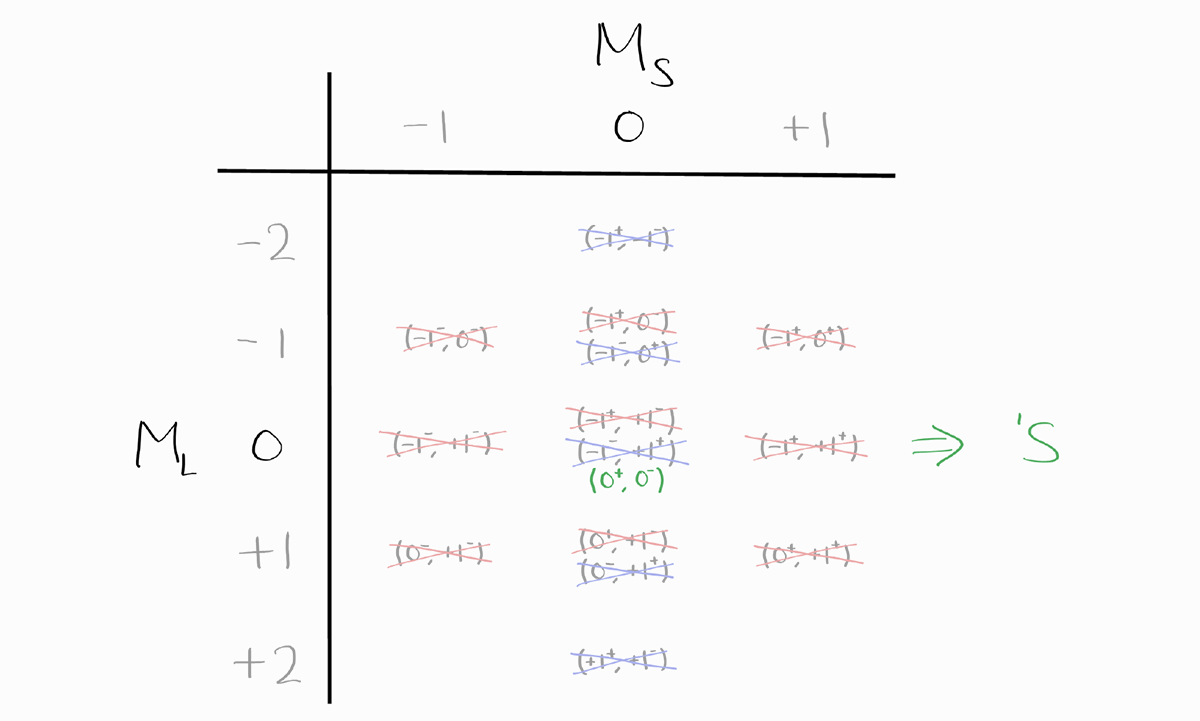
The last term symbol is $^1S$, where $M_S = 0$ and $M_L = 0$ thus $S = 0$ and $L = 0$.

These are the term symbols:

We have yet to fully specify these term symbols, notably the value of $J$. Recall how $J$ can have the values $\left|L - S\right|,\,\cdots,\,L + S$.

For $^3P$ ($L = 1$ and $S = 1$), $J_{\text{min}} = 0$ and $J_{\text{max}} = 2$. Therefore, $J = 2,\, 1,\, 0$ and the term symbols are $^3P_2$, $^3P_1$, and $^3P_0$.

For $^1D$ ($L = 2$ and $S = 0$), $J_{\text{min}} = 2$ and $J_{\text{max}} = 2$. Therefore, $J = 2$ and the term symbol is $^1D_2$.

For $^1S$ ($L = 0$ and $S = 0$), $J_{\text{min}} = 0$ and $J_{\text{max}} = 0$. Therefore, $J = 0$ and the term symbol is $^1S_0$.

Therefore, the term symbols for $1s^22s^22p^2$ carbon, or $np^2$ in general, are as follows.

Table of Possible Term Symbols

With the above procedure, a table of the term symbols for various electron configurations can be prepared.

Electron configuration	Term symbols (excluding $J$)
$s^1$	$^2S$
$p^1$; $p^5$	$^2P$
$p^2$; $p^4$	$^3P$, $^1D$, $^1S$
$p^3$	$^4S$, $^2D$, $^2P$
$d^1$; $d^9$	$^2D$
$d^2$; $d^8$	$^3F$, $^3P$, $^1G$, $^1D$, $^1S$
$d^3$; $d^7$	$^4F$, $^4P$, $^2H$, $^2G$, $^2F$, $^2D(\text{two})$, $^2P$
$d^4$; $d^6$	$^5D$, $^3H$, $^3G$, $^3F(\text{two})$, $^3D$, $^3P(\text{two})$, $^1I$, $^1G(\text{two})$, $^1F$, $^1D(\text{two})$, $^1S(\text{two})$
$d^5$	$^6S$, $^4G$, $^4F$, $^4D$, $^4P$, $^2I$, $^2H$, $^2G(\text{two})$, $^2F(\text{two})$, $^2D(\text{three})$, $^2P$, $^2S$
$s^2$; $\,p^6$; $\,d^{10}$; $\,\cdots$	$^1S$

There are three things to note about this table.

First, some electron configuration produces two or more of the same term symbol. This is the exception where two or more energy states of the same electron configuration can have the same $L$, $M_L$, $S$, and $M_S$. For these cases, electron configuration alone is not a suitable substitute to energy when describing energy states (and levels).

Second, electron configurations consisting of only filled subshells are always $^1S$, as all $m_l$ and $m_s$ cancel out between all electrons, resulting in $M_L = 0$ and $M_S = 0$. In fact, like $M_L$ and $M_S$, $M_J$ always equals zero. Thus, $J = 0$ and their term symbol is indeed always $^1S_0$.

The last and most important point is about electron holes, which are the absense of electrons. Electron configurations with some electron holes (lack of electrons) have the same term symbols as those with the same number of electrons in the same subshell. In other words, adding $n$ electrons to an empty subshell is the same (with respect to angular momentum) as removing $n$ electrons from a full subshell. Holes act like electrons; they contribute to the overall angular momenta in the same way.

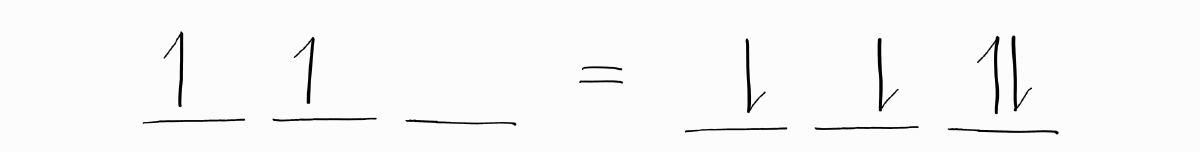
Therefore, not only is it acceptable to replace electron holes with electrons to calculate $L$ and $S$, it is often easier to do so.

Example 2: Excited $1s^22s^22p^43p^2$ Neon

Let us apply three useful points that we have learned until now on an excited neon configuration of $1s^22s^22p^43p^2$.

1. Completely filled subshells do not contribute to the overall $M_L$ and $M_S$, and thus can be ignored when determining term symbols.
2. Replace electron holes with electrons when calculating $L$ and $S$.
3. (From part 2) The addition of two angular momenta characterized by quantum numbers $j_1$ and $j_2$ results in a total angular momentum whose quantum number $J$ has the possible values $ J=\left|j_1 - j_2\right|,\,\cdots,\,j_1 + j_2$

From the $1s^22s^22p^43p^2$ configuration, we can ignore completely filled subshells and only deal with $2p^43p^2$ - all thanks to point 1.

With point 2, the $2p^43p^2$ configuration can be replaced with the $2p^23p^2$ configuration by replacing electron holes in the $2p$ subshell with electrons.

We are left with the $2p^23p^2$ configuration. This configuration consist of the $2p^2$ configuration and the $3p^2$ configuration. For a $np^2$ configuration (equivalent electrons), the term symbols are (without $J$) $^3P$, $^1P$, and $^1S$ (as we have calculated for ground state carbon). Between $2p^2$ and $3p^2$ subshells (which are non-equivalent electrons), the $L$ and $S$ of the term symbols (denoted $l_i$ and $s_i$ below) can be “added” according to point 3 to produce new term symbols characterizing $2p^23p^2$ as a whole.

A. Adding $^3P$ and $^3P$

Term Symbol	$l_i$	$s_i$
$^3P$	1	1
$^3P$	1	1

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
1	1	0	2	0, 1, 2

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
1	1	0	2	0, 1, 2

⇒ $^5D$, $^5P$, $^5S$, $^3D$, $^3P$, $^3S$, $^1D$, $^1P$, and $^1S$

B. Adding $^3P$ and $^1D$

Term Symbol	$l_i$	$s_i$
$^3P$	1	1
$^1D$	2	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
1	2	1	3	1, 2, 3

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
1	0	1	1	1

⇒ $^3F$, $^3D$, and $^3P$

C. Adding $^1D$ and $^3P$

Same as B. Adding $^3P$ and $^1D$.

⇒ $^3F$, $^3D$, and $^3P$

D. Adding $^3P$ and $^1S$

Term Symbol	$l_i$	$s_i$
$^3P$	1	1
$^1S$	0	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
1	0	1	1	1

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
1	0	1	1	1

⇒ $^3P$

E. Adding $^1S$ and $^3P$

Same as D. Adding $^3P$ and $^1S$.

⇒ $^3P$

F. Adding $^1D$ and $^1D$

Term Symbol	$l_i$	$s_i$
$^1D$	2	0
$^1D$	2	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
2	2	0	4	0, 1, 2, 3, 4

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
0	0	0	0	0

⇒ $^1G$, $^1F$, $^1D$, $^1P$, and $^1S$

G. Adding $^1D$ and $^1S$

Term Symbol	$l_i$	$s_i$
$^1D$	2	0
$^1S$	0	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
2	0	2	2	2

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
0	0	0	0	0

⇒ $^1D$

H. Adding $^1S$ and $^1D$

Same as G. Adding $^1D$ and $^1S$.

⇒ $^1D$

I. Adding $^1S$ and $^1S$

Term Symbol	$l_i$	$s_i$
$^1S$	0	0
$^1S$	0	0

$l_1$	$l_2$	$L_{\text{min}}$	$L_{\text{max}}$	$L$
0	0	0	0	0

$s_1$	$s_2$	$S_{\text{min}}$	$S_{\text{max}}$	$S$
0	0	0	0	0

⇒ $^1S$

As a result, the term symbols for $1s^22s^22p^43p^2$ are:

$^5D$, $^5P$, $^5S$, $^3F$ (two), $^3D$ (three), $^3P$ (five), $^3S$, $^1G$, $^1F$, $^1D$ (four), $^1P$ (two), and $^1S$ (three).

If you count the number of states of each of these term symbols, it adds up to $225 = 15\times 15$, which checks out as it is equal to the number of microstates for $1s^22s^22p^43p^2$.

Hund’s Rule and Ground State

Until now, we were occupied with finding out all possible term symbols from an electron configuration. An important question to ask is “what is the most stable term symbol among all term symbols?” In other words, “what is the ground state of an atom?”¹

Three empirical rules by spectroscopist Friederich Hund allow us to obtain the ground state term symbol.

1. The term symbol with the largest value of $S$ is the most stable.
2. For term symbols with the same value of $S$, the term symbol with the largest value of $L$ is the most stable.

3. For term symbols with the same value of $S$ and $L$, $J$ is used to determine the most stable term symbol.

   1. For a subshell less than half-filled, the term symbol with the smallest $J$ is the most stable.
   2. For a subshell more than half-filled, the term symbol with the largest $J$ is the most stable.

As an example, the term symbols of ground configuration $1s^22s^22p^2$ carbon are $^1S_0$, $^3P_2$, $^3P_1$, $^3P_0$, and $^1D_2$. The term symbols with the largest $S$ are $^3P_2$, $^3P_1$, and $^3P_0$.

Among those term symbols, all three have the same $L$.

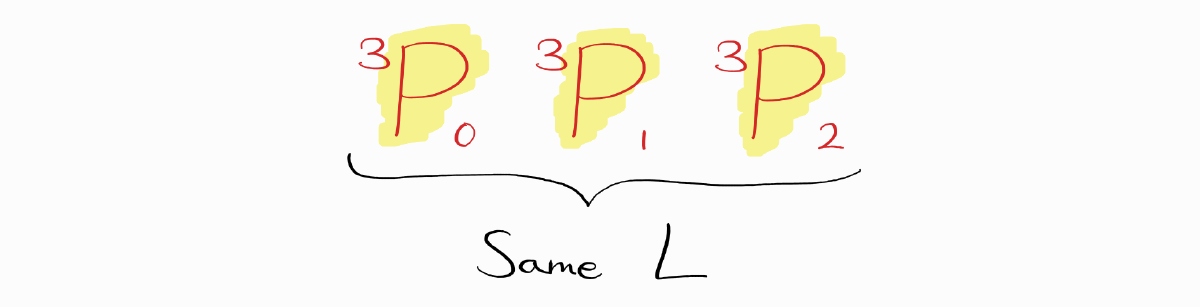
Therefore, we move on to the third rule and use $J$ to determine the ground state term symbol. Because the $2p$ subshell is less than half-filled, we choose the term symbol with the smallest value of $J$.

As a result, $^3P_0$ is the ground state term symbol for carbon.

These term symbols can be shown with an energy diagram similar to that at the end of Part 2.

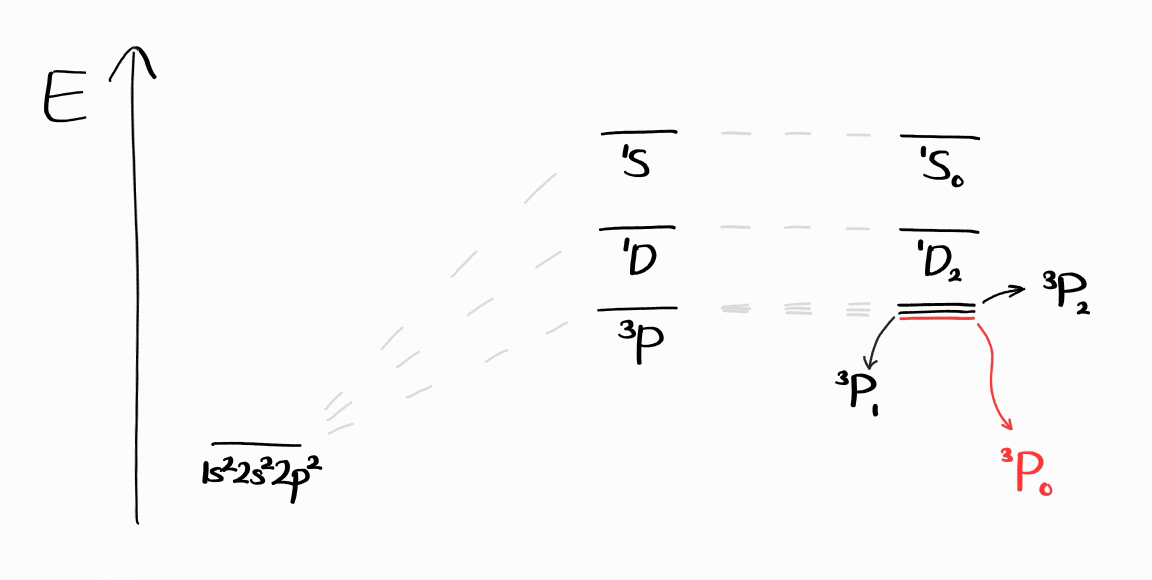
When obtaining the ground state term symbol, it is not necessary to obtain all term symbols. There is an easier way that involves finding the microstate that is related to the ground state term symbol. We first start with the microstates with the largest value of $M_S$, in order to maximize $S$. This is the general chemistry version of Hund’s Rules, and is deeply related to the quantum mechanical, spectroscopic version of Hund’s Rules as well.

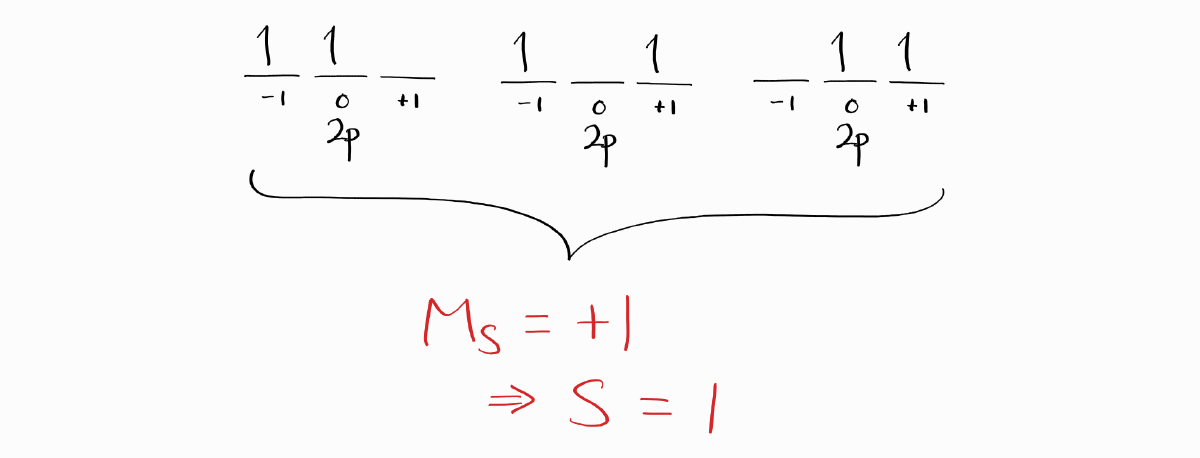
Of those microstates, we choose the microstate with the largest value of $M_L$, in order to maximize $L$.

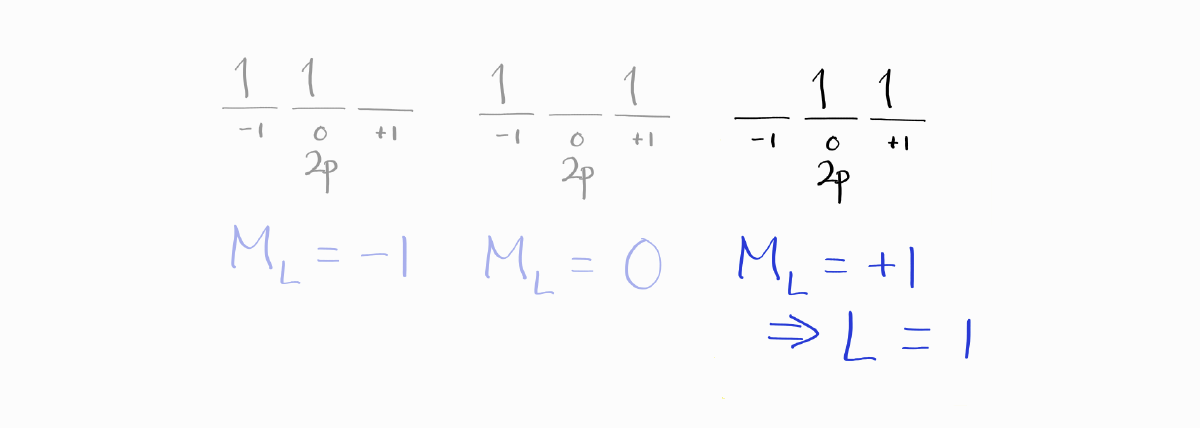
As $S = 1$ and $L = 1$, the term symbol without $J$ is $^3P$. Calculating the remaining $J$ and choosing the right value according to Hund’s Law leaves us with the same ground state term symbol: $^3P_0$.

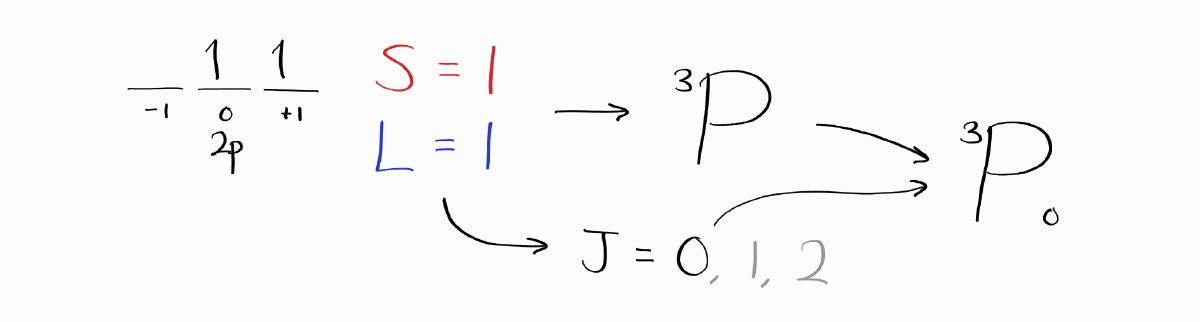
A more complicated example would be manganese, with a ground state electron configuration of $\left[\text{Ar}\right]3d^54s^2$. In total, there are 252 microstates for this configuration, which results in 16 term symbols. It is an incredibly difficult and error-prone task to obtain the ground state term symbol by calculating all possible term symbols. However, if we use the method above, we can obtain the ground state term symbol of manganese with incredible ease.

We start with the microstate with the largest value of $M_S$.

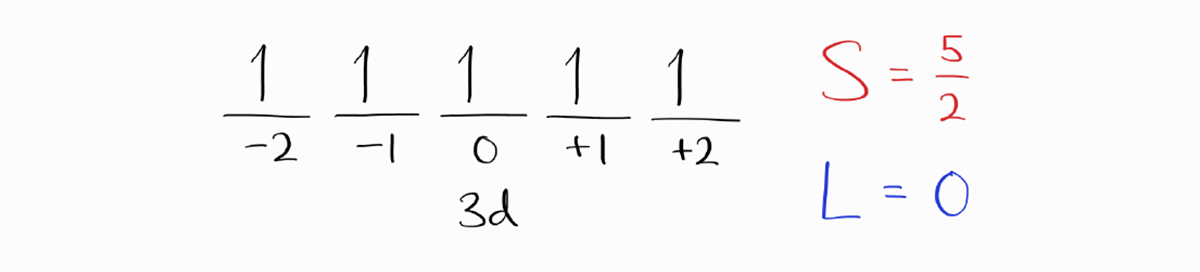
Incidently enough, there is only one microstate left, which leaves us with $M_L = 0$. Therefore, $L=0$ and the term symbol (without $J$) is $^6S$.

As the $3d$ subshell is exactly half-filled, it presents a dilemma with determining $J$ using Hund’s Rules. However, the only possible value of $J$ is $5/2$, so the ground state term symbol of $J$ is $^6S_{5/2}$.

Hund’s Rules works very well for ground state electron configuration, but may fail for other excited configurations. In addition, Hund’s Rules cannot be reliably used to determine the energy order between the term symbols. In essence, use Hund’s Rules only for the ground state of an atom.

Conclusion

When obtaining all term symbols of an electron configuration:

1. Ignore all filled subshells.
2. For each subshell, if the subshell is more than half-filled, replace electron holes with electrons.
3. Calculate $l_i$ and $s_i$ for subshells with equivalent electrons by setting up a table of microstates or by using the table of term symbols provided in your textbook.
4. Calculate the total $L$ and $S$ by adding the $l_i$ and $s_i$ of all subshells (non-equivalent electrons)
5. Calculate $J$ for each combination of $L$ and $S$

When obtaining the ground state term symbol with all term symbols already known - Hund’s Rules:

1. The term symbol with the largest value of $S$ is the most stable.
2. For term symbols with the same value of $S$, the term symbol with the largest value of $L$ is the most stable.

3. For term symbols with the same value of $S$ and $L$, $J$ is used to determine the most stable term symbol.

   1. For a subshell less than half-filled, the term symbol with the smallest $J$ is the most stable.
   2. For a subshell more than half-filled, the term symbol with the largest $J$ is the most stable.

When obtaining the ground state term symbol without knowing the term symbols:

1. Start with microstates with the maximum value of $M_S$. This $M_S = S$.
2. Choose the microstate with the maximum value of $M_L$. This $M_L = L$.
3. Calculate $J$ with $L$ and $S$. Choose the correct $J$ according to Hund’s Rules.

Footnotes

1. Most textbooks refer to the most stable term symbol as “the ground state”, even though it should really be refered to as “the ground level”. In line with most textbooks, this article refers to such ground level term symbol as “the ground state term symbol”. ↩